HP 48gII - Manual (Page 459)

Page 13-24
∑ ∑
∞
+ = =
− ⋅ + − ⋅ =
1
) (
0
) (
) (
!
) (
) (
!
) (
) (
k n
n
o
o
n k
n
n
o
o
n
x x
n
x f
x x
n
x f
x f
,
i.e.,
). ( ) ( ) ( x R x P x f
k k
+ =
The polynomial P
k
(x) is referred to as Taylor’s polynomial. The order of the
residual is estimated in terms of a small quantity h = x-x
0
, i.e., evaluating the
polynomial at a value of x very close to x
0
. The residual if given by
1
) 1 (
!
) (
) ( +
+
⋅ = k
k
k
h
k
f
x R
ξ
,
where ξ is a number near x = x
0
. Since ξ is typically unknown, instead of an
estimate of the residual, we provide an estimate of the order of the residual in
reference to h, i.e., we say that R
k
(x) has an error of order h n+1 , or R ≈ O(h k+1 ).
If h is a small number, say, h<<1, then h k+1 will be typically very small, i.e.,
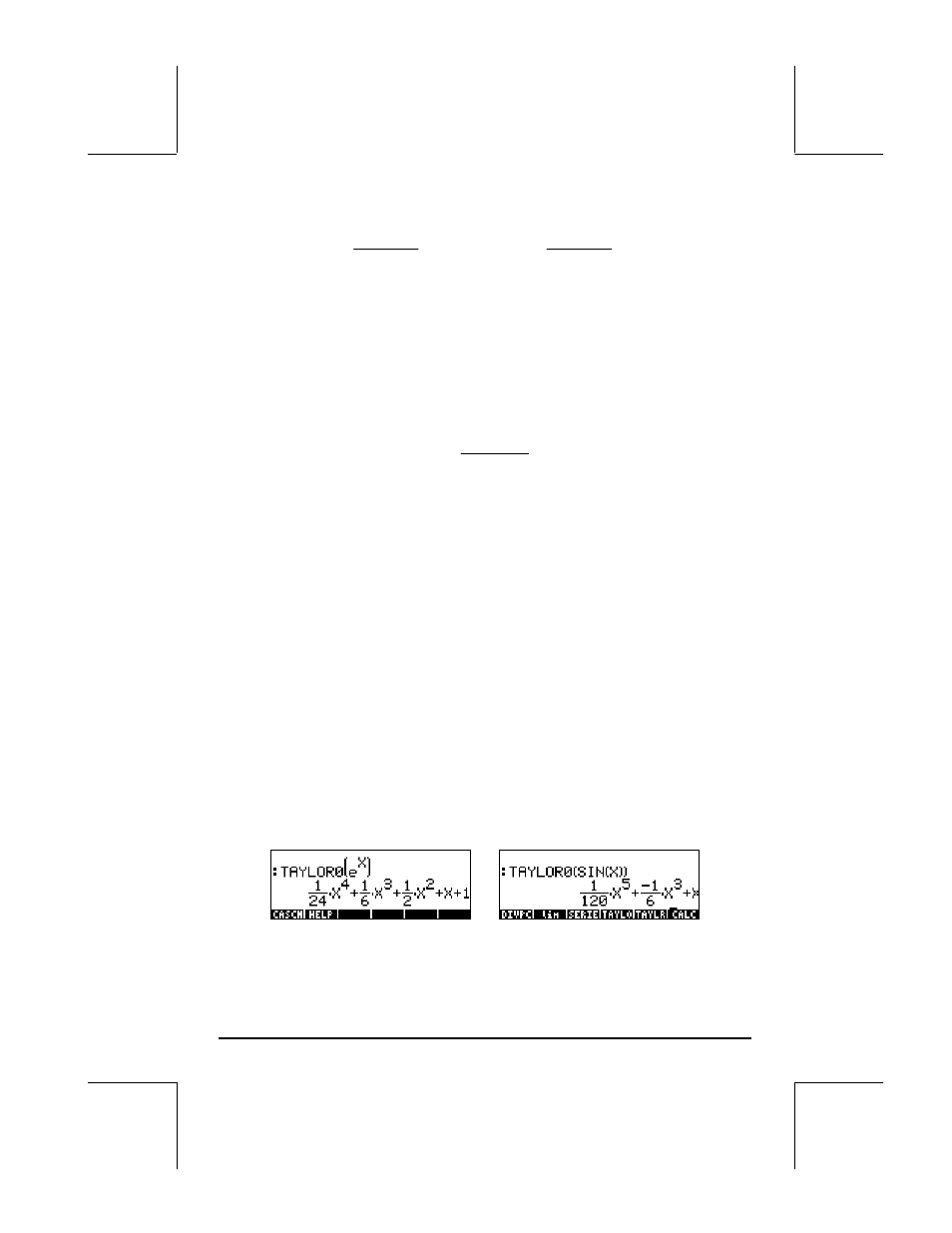
h k+1 < k << …<< h << 1. Thus, for x close to x
0
, the larger the number of
elements in the Taylor polynomial, the smaller the order of the residual.
Functions TAYLR, TAYLR0, and SERIES
Functions TAYLR, TAYLR0, and SERIES are used to generate Taylor
polynomials, as well as Taylor series with residuals. These functions are
available in the CALC/LIMITS&SERIES menu described earlier in this Chapter.
Function TAYLOR0 performs a Maclaurin series expansion, i.e., about X = 0,
of an expression in the default independent variable, VX (typically ‘X’). The
expansion uses a 4-th order relative power, i.e., the difference between the
highest and lowest power in the expansion is 4. For example,