HP 48gII - Manual (Page 485)

Page 16-7
Allow the calculator about ten seconds to produce the result: ‘X^2 = X^2’.
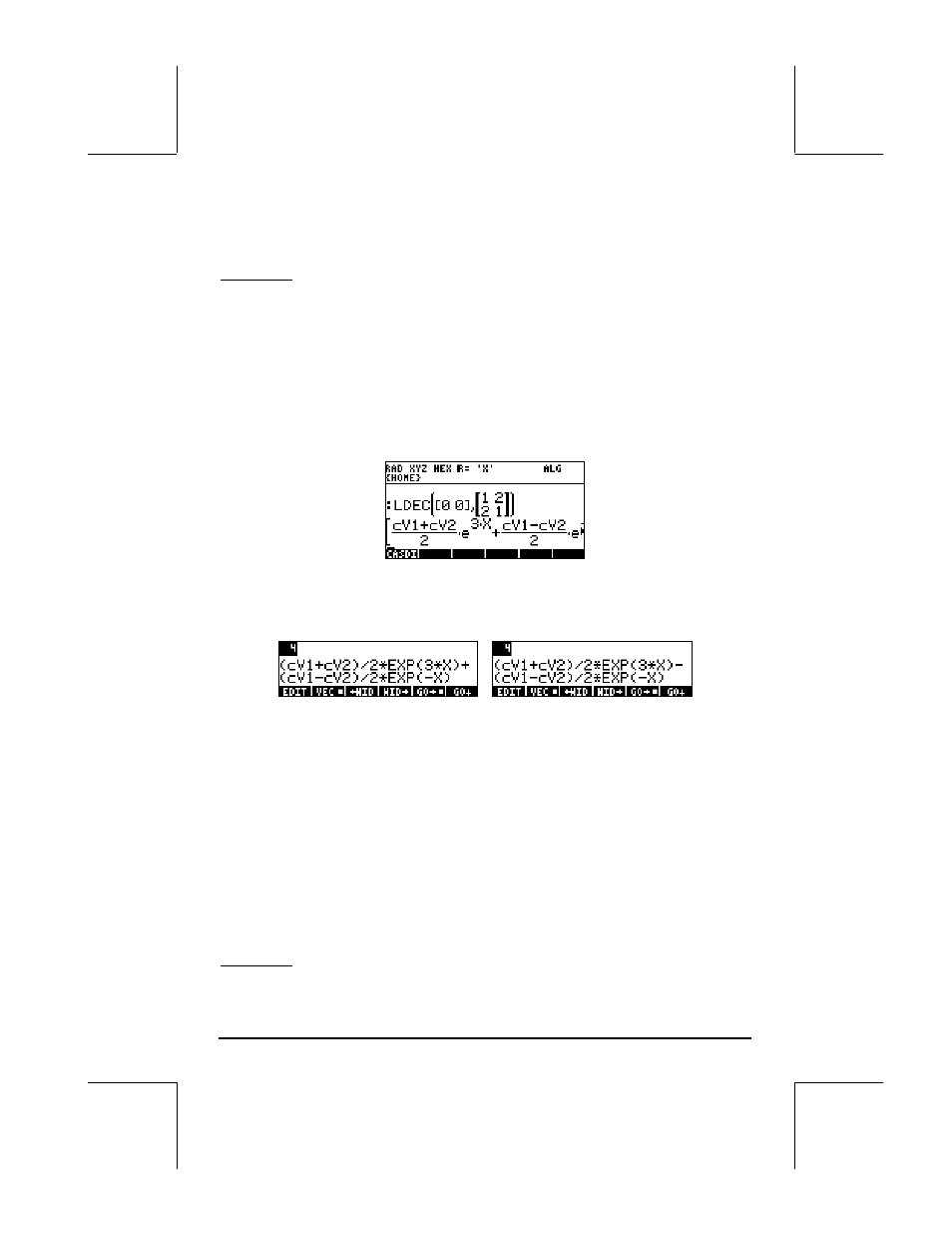
Example 3 - Solving a system of linear differential equations with constant
coefficients.
Consider the system of linear differential equations:
x
1
’(t) + 2x
2
’(t) = 0,
2x
1
’(t) + x
2
’(t) = 0.
In algebraic form, this is written as: A⋅x’(t) = 0, where






=
1 2
2 1
A
. The
system can be solved by using function LDEC with arguments [0,0] and matrix
A, as shown in the following screen using ALG mode:
The solution is given as a vector containing the functions [x
1
(t), x
2
(t)]. Pressing
˜ will trigger the Matrix Writer allowing the user to see the two
components of the vector. To see all the details of each component, press the
@EDIT! soft menu key. Verify that the components are:
Function DESOLVE
The calculator provides function DESOLVE (Differential Equation SOLVEr) to
solve certain types of differential equations. The function requires as input the
differential equation and the unknown function, and returns the solution to the
equation if available. You can also provide a vector containing the
differential equation and the initial conditions, instead of only a differential
equation, as input to DESOLVE. The function DESOLVE is available in the
CALC/DIFF menu. Examples of DESOLVE applications are shown below
using RPN mode.
Example 1 – Solve the first-order ODE: