Function trace – HP 48gII User Manual
Page 339
Page 11-13
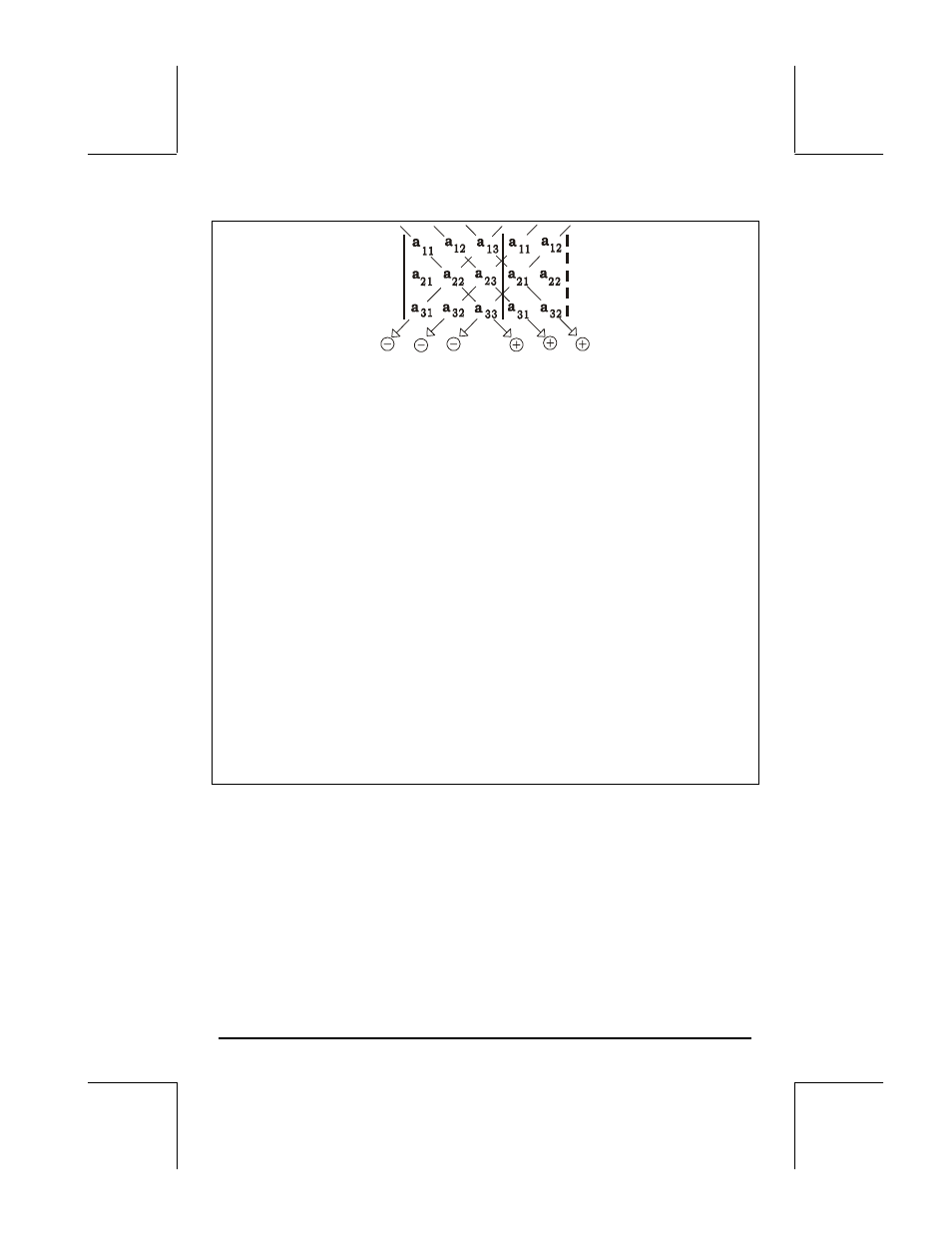
For square matrices of higher order determinants can be calculated by using
smaller order determinant called cofactors. The general idea is to “expand” a
determinant of a n
×n matrix (also referred to as a n×n determinant) into a sum
of the cofactors, which are (n-1)
×(n-1) determinants, multiplied by the elements
of a single row or column, with alternating positive and negative signs. This
“expansion” is then carried to the next (lower) level, with cofactors of order (n-
2)
×(n-2), and so on, until we are left only with a long sum of 2×2
determinants. The 2
×2 determinants are then calculated through the method
shown above.
The method of calculating a determinant by cofactor expansion is very
inefficient in the sense that it involves a number of operations that grows very
fast as the size of the determinant increases. A more efficient method, and
the one preferred in numerical applications, is to use a result from Gaussian
elimination. The method of Gaussian elimination is used to solve systems of
linear equations. Details of this method are presented in a later part of this
chapter.
To refer to the determinant of a matrix
A, we write det(A). A singular matrix
has a determinant equal to zero.
Function TRACE
Function TRACE calculates the trace of square matrix, defined as the sum of
the elements in its main diagonal, or
∑
=
=
n
i
ii
a
tr
1
)
(A
.
Examples:
