Curl, Irrotational fields and potential function – HP 48gII User Manual
Page 476
Page 15-5
Curl
The curl of a vector field F(x,y,z) = f(x,y,z)i+g(x,y,z)j+h(x,y,z)k, is defined by
a “cross-product” of the del operator with the vector field, i.e.,
[ ]
[ ]
[ ]
)
,
,
(
)
,
,
(
)
,
,
(
z
y
x
h
z
y
x
g
z
y
x
f
z
y
x
curl
∂
∂
∂
∂
∂
∂
=
×
∇
=
k
j
i
F
F
∂
∂
−
∂
∂
+
∂
∂
−
∂
∂
+
∂
∂
−
∂
∂
=
z
g
y
h
x
h
z
f
z
g
y
h
k
j
i
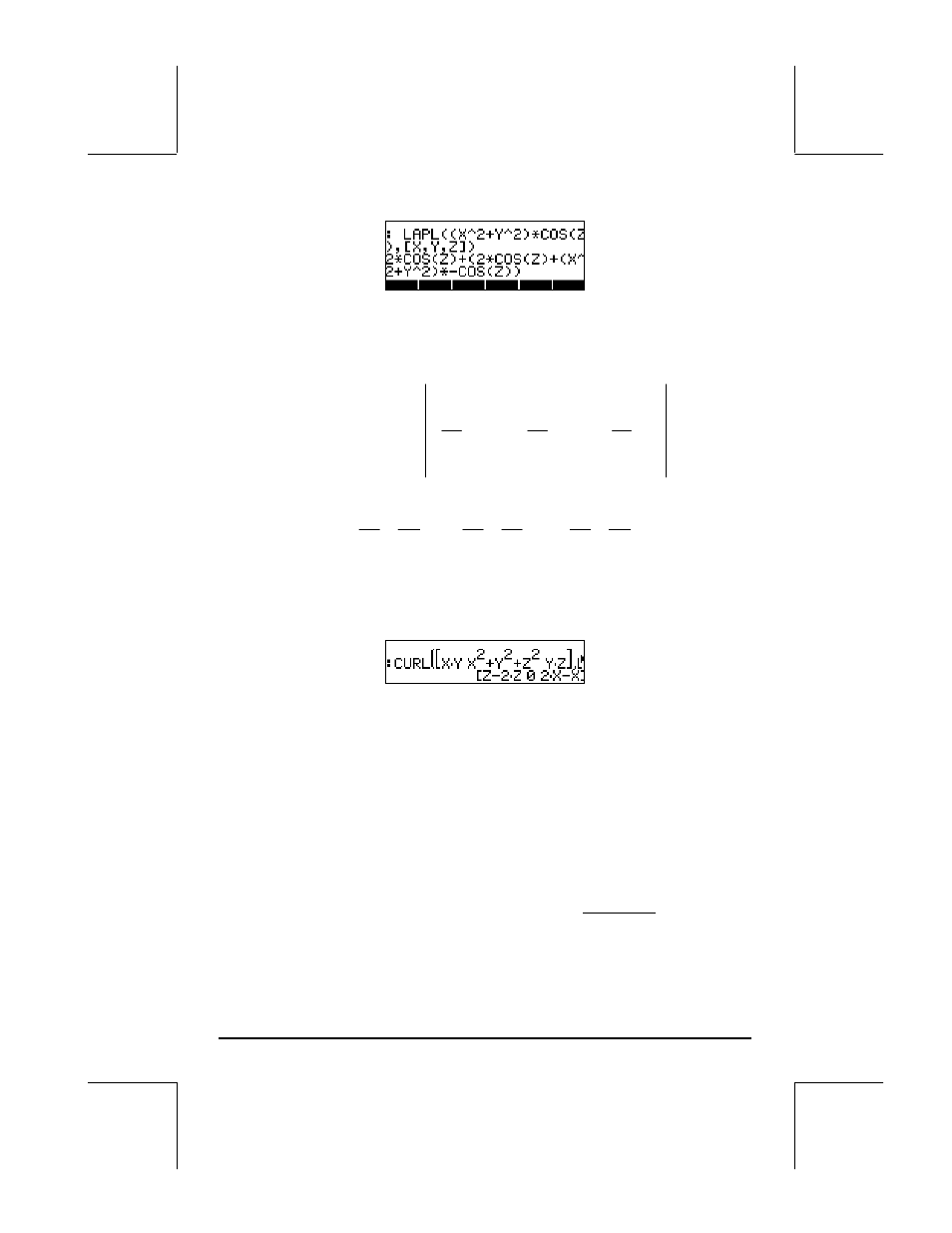
The curl of vector field can be calculated with function CURL. For example,
for the function F(X,Y,Z) = [XY,X
2
+Y
2
+Z
2
,YZ], the curl is calculated as follows:
Irrotational fields and potential function
In an earlier section in this chapter we introduced function POTENTIAL to
calculate the potential function
φ(x,y,z) for a vector field, F(x,y,z) = f(x,y,z)i+
g(x,y,z)j+ h(x,y,z)k, such that F = grad
φ = ∇φ. We also indicated that the
conditions for the existence of
φ, were: ∂f/∂y = ∂g/∂x, ∂f/∂z = ∂h/∂x, and
∂g/∂z = ∂h/∂y. These conditions are equivalent to the vector expression
curl F =
∇×F = 0.
A vector field F(x,y,z), with zero curl, is known as an irrotational field. Thus,
we conclude that a potential function
φ(x,y,z) always exists for an irrotational
field F(x,y,z).
