PASCO ME-9502 Statics System - Manual (Page 87)

®
M o d e l N o . M E - 9 5 0 2 E x p . 1 5 : F o r c e s o n a B o o m
0 1 2 - 1 2 8 7 6 B 83
Exp. 15: Forces on a Boom
Equipment Needed
Theory
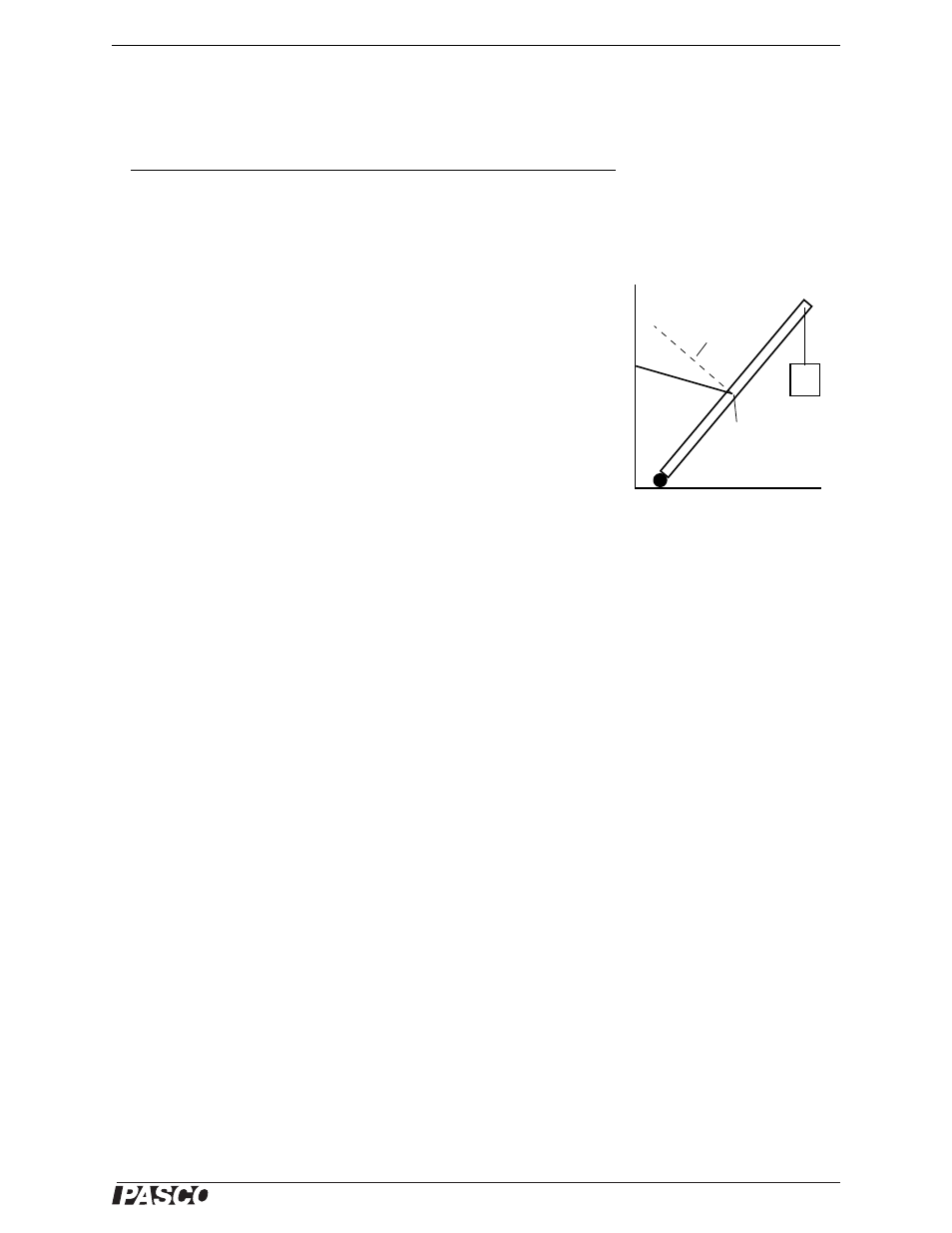
A boom supported by a cable has a mass suspended at its upper end. The
lower end of the boom is supported by a pivot.
For example, if the mass is 100 kg and the boom has a mass of 50 kg, what is
the tension, T, in the cable? Assume that the cable is attached at the boom’s
center of mass and is at an angle relative to the boom. The boom is at an angle
of 50° to the horizontal.
For the boom to be in equilibrium, all of the translational forces (F
x
and F
y
)
and all of the torques must add up to zero. One torque is produced by the ten-
sion in the cable. Another torque is produced by the weight of the beam. A
third torque is produced by the weight of the hanging mass.
where W is the weight of the hanging mass, L is the lever arm from the pivot point to the place where the hanging
mass is attached, W
boom
is the weight of the boom, L
cm
is the lever arm from the pivot point to the center of mass,
 is the angle of the boom, T is the tension in the cable, and  is the angle of the cable relative to the normal of the
boom.
If the boom is in equilibrium, the net torque is zero. The expression for the tension, T, in the cable becomes:
Item Item
Statics Board Mounted Spring Scale and Pulley
Balance Arm and Protractors) Thread
Mass and Hanger Set
Fig. 15.1: Suspended Mass
Cable
Mass
c.o.m.
Pivot
Boom
normal

clockwise
WL

cos
 
W
cm
L
cm

cos
 
+ =

counterclockwise
TL
cm

cos =
T
WL

cos
 
W
cm
L
cm

cos
 
+
L
cm

cos
----------------------------------------------------------------------- =