Exp. 11b: minimum period of a physical pendulum, Theory – PASCO ME-9502 Statics System User Manual

Page 67

M o d e l N o . M E - 9 5 0 2

E x p . 1 1 B : M i n i m u m P e r i o d o f a P h y s i c a l P e n d u l u m

0 1 2 - 1 2 8 7 6 B

Exp. 11B: Minimum Period of a Physical Pendulum

Equipment Needed

Theory

The period of oscillation for a physical pendulum can be written as
follows:

where I is the moment of inertia (rotational inertia) for the physical
pendulum, L

is the perpendicular distance from the axis at the pivot

point to the parallel axis at the center of mass, cm, and m is the mass
of the pendulum.

The moment of inertia, I

, for a rectangular-type rod about its center

of mass is:

where a is the length and b is the thickness of the rectangular-type
rod. However, if the length, a, is much greater than the thickness, b,
then the following can be used as a very good approximation of the
moment of inertia around the center of mass:

where m is the mass and L is the length of the rod.

If the rod pivots around any other axis that is parallel to the axis through the center of mass, the Parallel Axis The-
orem states that the moment of inertia about the parallel axis, I

parallel

, is the sum of the moment of inertia around

the center of mass, I

, plus mL

, where m is the mass of the rod and L

is the perpendicular distance from the

center of mass to the pivot point, or

The formula for the period of oscillation becomes

At what distance, L

, does the period of oscillation, T, become a minimum?

In this experiment you will determine the distance, L

, from the pivot point to the center of mass that gives the

minimum period of oscillation for the physical pendulum.

Item

Statics Board

Balance Arm

Stopwatch (ME-1234)

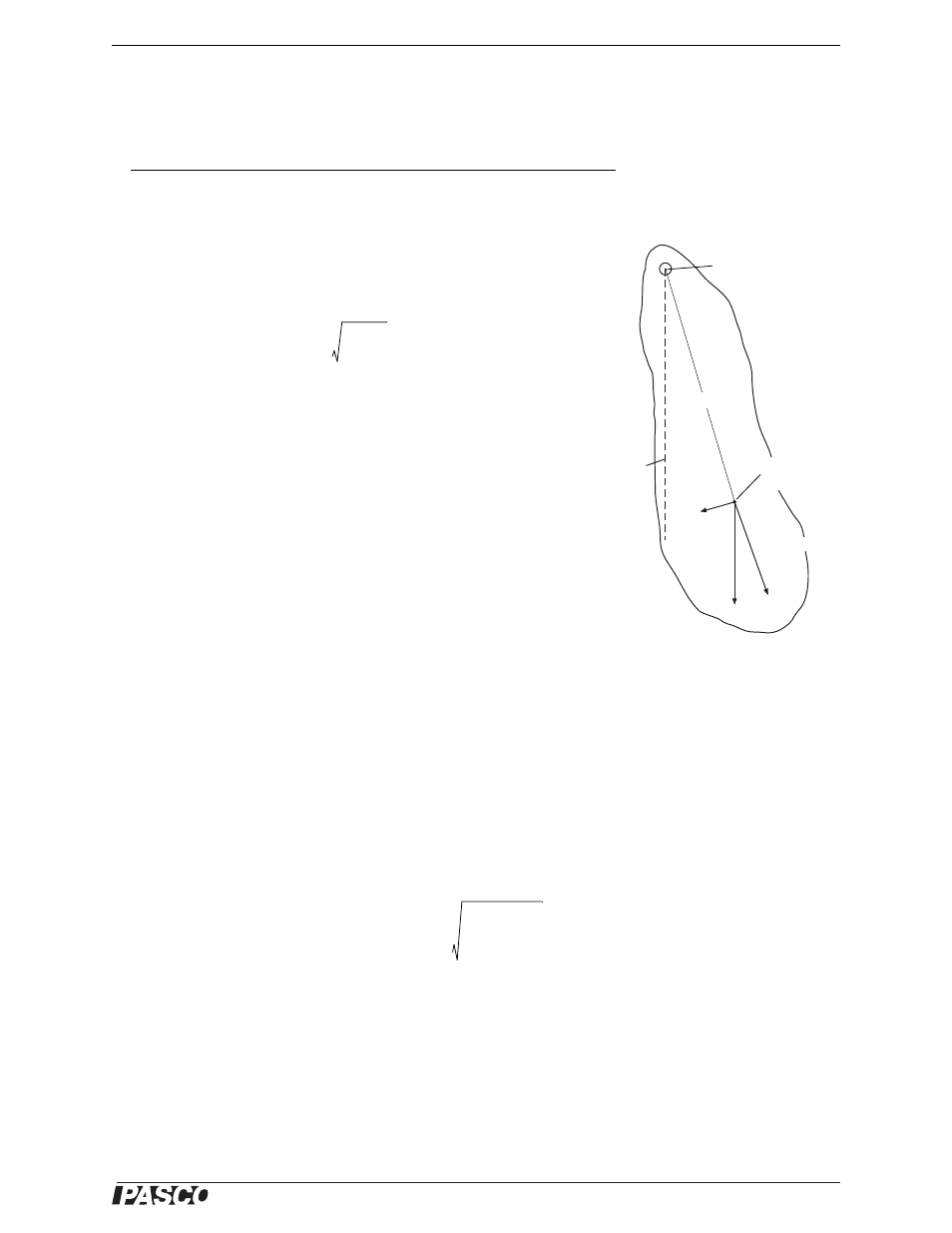
Figure 11.5: Physical Pendulum



mg sin



mg cos



Equilibrium

position

Pivot
point

Center of

mass



-----------------

------m a





------mL

parallel

------mL



------L

-------------------------------