PASCO ME-9502 Statics System - Manual (Page 51)

®
M o d e l N o . M E - 9 5 0 2 E x p . 9 : S i m p l e H a r m o n i c M o t i o n – M a s s o n a S p r i n g
0 1 2 - 1 2 8 7 6 B 47
Exp. 9: Simple Harmonic Motion–Mass on a Spring
Equipment Needed
Theory
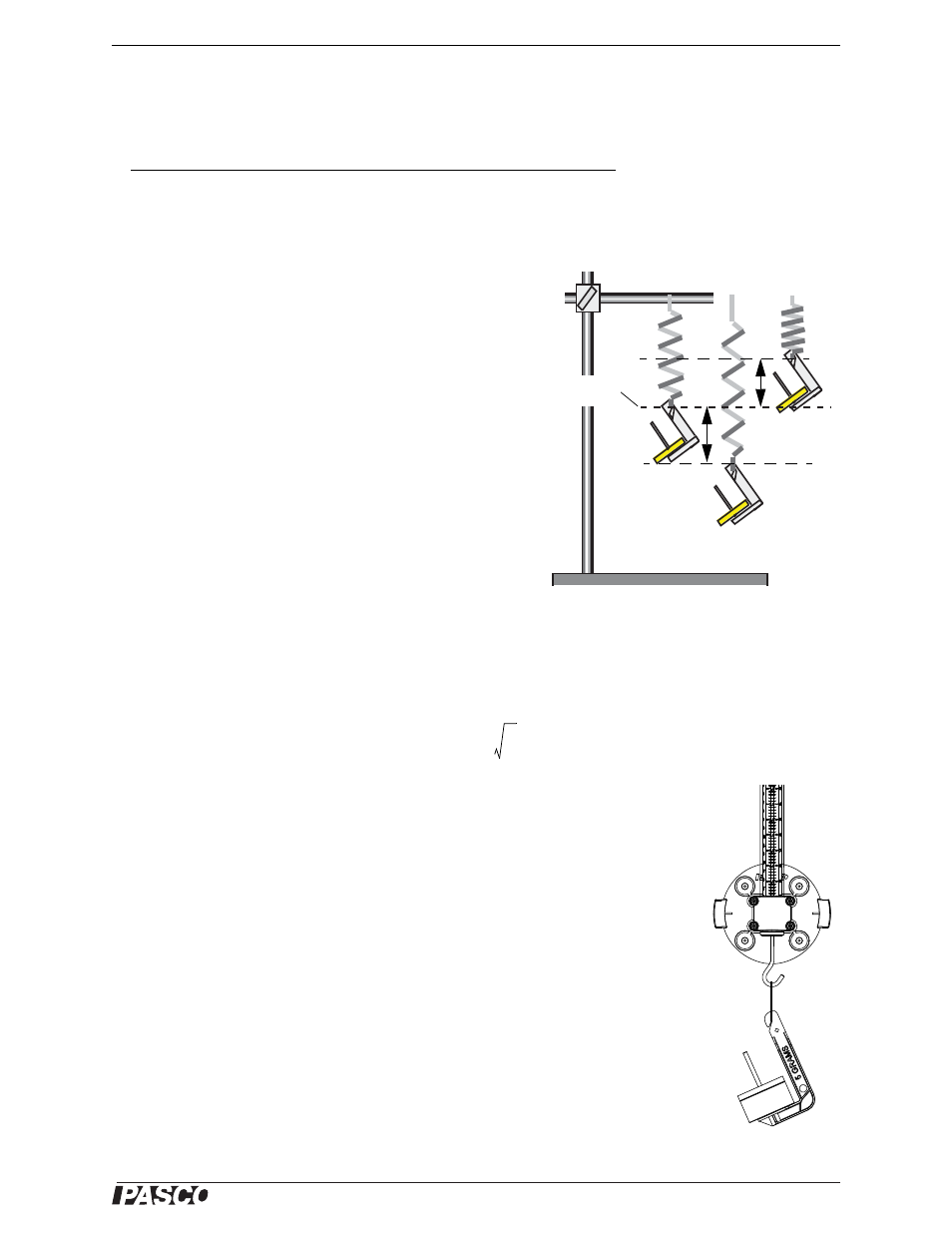
Imagine a mass hanging from a spring. At rest, the mass hangs in
a position such that the spring force just balances the gravita-
tional force on the mass (its weight). When the mass is pulled
below this original point (called the equilibrium position), the
spring exerts a force to pull it back up. When the mass is above
this original point, gravity pulls it down. The net force on the
mass is therefore a restoring force because it always acts to
accelerate the mass back toward its equilibrium position.
Previously you may have investigated Hooke’s Law, which states
that the force exerted by a spring is proportional to the distance
beyond its normal length to which it is stretched. (This also is
true for the compression of a spring.) This relationship is stated
as F = -kx, where F is the force exerted by the spring, x is the
displacement of the end of the spring from the equilibrium posi-
tion, and k is the constant of proportionality, called the spring
constant.
Whenever an object is acted on by a restoring force that is proportional to the displacement of the object from its
equilibrium position, the resulting motion is called Simple Harmonic Motion (SHM). When the simple harmonic
motion of a mass, M, on a spring is analyzed mathematically using Newton’s Second Law (and calculus), the
period of the motion, T, is as follows:
The period, T, is the amount of time for one complete oscillation (down-up-down). In this
experiment you will investigate this equation for the period of simple harmonic motion.
Procedure
1. Measure and record k, the spring constant for the spring in the Spring Scale (see Exp:
Hooke’s Law).
• spring constant, k = _________________ (N/m)
2. Mount the Spring Scale on the Statics Board so that the scale is perfectly vertical. Use
thread to hang a mass hanger from the scale, and add 120 g of mass to the hanger (for
a total hanging mass of 125 g (0.125 kg).
• Practice the following: Pull the mass hanger down several centimeters and release it
smoothly so that the mass hanger oscillates up and down without moving from side to
side.
Item Item
Statics Board Mounted Spring Scale
Mass and Hanger Set Thread
Stopwatch (ME-1234)
Equilibrium
position
Figure 9.1: Spring Constant
T 2
 M
k
----- =
Figure 9.2: Setup
Spring
Scale
120 g
Mass
hanger