PASCO ME-9502 Statics System - Manual (Page 47)

®
M o d e l N o . M E - 9 5 0 2 S l i d i n g F r i c t i o n o n a n I n c l i n e d P l a n e
0 1 2 - 1 2 8 7 6 B 43
Questions
1. In trials 1 through 6, what happens to the sliding friction as the normal force increases?
2. In trials 1 through 6, what happens to the coefficient of friction as the normal force increases?
3. How does the sliding friction for the large wood surface compare to the sliding friction for the large felt sur-
face? How does the sliding friction for the small wood surface compare to the sliding friction for the small felt
surface?
4. Based on your measurements, does the sliding friction between two objects depend on the materials that are in
contact?
5. How does the sliding friction for the large wood surface compare to the sliding friction for the small wood
surface? How does the sliding friction for the large felt surface compare to the sliding friction for the small
felt surface?
6. Based on your measurements, does the sliding friction between two objects depend on the area of contact
between the objects?
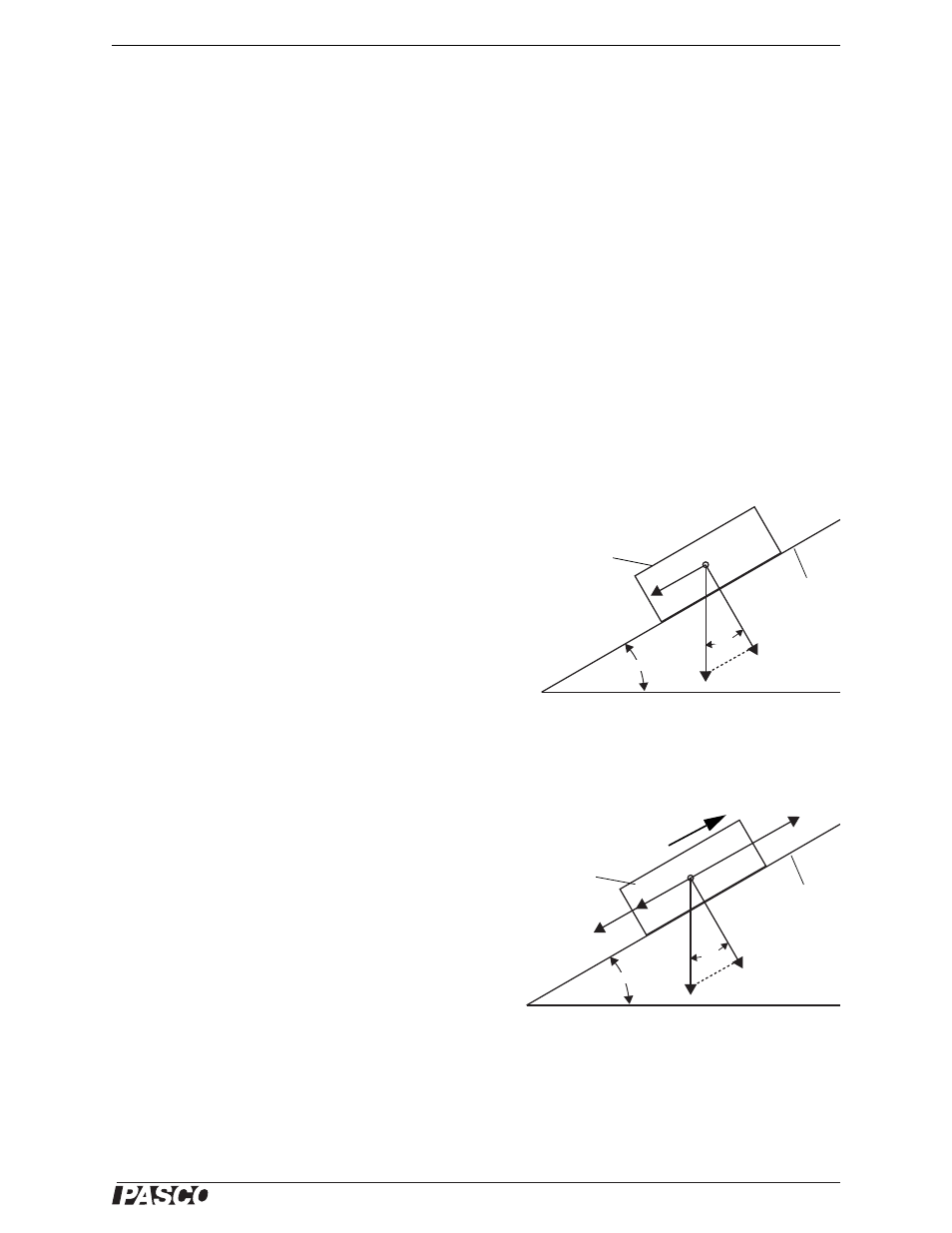
Sliding Friction on an Inclined Plane
If the Friction Block is not on a horizontal surface, will the
coefficient of sliding friction,

k
, be different?
When an object is on the Inclined Plane at an angle, one compo-
nent of the object’s weight (F = mg) is parallel to the surface of
the plane (F

), and another component of F is perpendicular to
the plane (F

. In theory, this perpendicular component is equal
to the normal force of the surface of the plane.
If there was no friction between the object and the plane, the
parallel component of the object’s weight would accelerate the
object down the plane. However, because there is friction
between the object and the plane, the force of friction (f =
F
N
)
opposes the parallel component of force. In other words, the vector for the force of friction would point up the
plane as the object slides down the plane.
Imagine that the object is being pulled up the plane by the
tension of a thread connected to a hanging mass. Would the
sliding friction (f
k
=

k
F
N
) oppose the parallel component of
the object’s weight, or would the vector for the sliding fric-
tion be in the same direction as the parallel component? Both
forces would point down the plane as the object is pulled up
the plane. If the object is pulled at a constant speed, then the
net force on the object is zero. Would the tension in the
thread, T, equal the sum of the parallel component and the
sliding friction?
Prediction
How will the sum of the parallel component of the block’s weight (F

) plus the sliding friction (f
k
) compare to the
weight of the hanging mass?
Figure 8.2: The Inclined Plane
F

F

Object

F

Inclined
plane


F

F
F 
Friction
Block
f
k
Direction
of motion.
Inclined
plane
T
Figure 8.3: Force Diagram