Exp. 11a: simple harmonic motion-physical pendulum, Theory, Exp. 11a: simple harmonic motion–physical pendulum – PASCO ME-9502 Statics System User Manual

Page 61

M o d e l N o . M E - 9 5 0 2

E x p . 1 1 A : S i m p l e H a r m o n i c M o t i o n – P h y s i c a l P e n d u l u m

0 1 2 - 1 2 8 7 6 B

Exp. 11A: Simple Harmonic Motion–Physical Pendulum

Equipment Needed

Theory

A simple pendulum is a mass on the end of a “massless” length of
string. A physical pendulum is any rigid body that pivots at some
point of the body so that it can rotate freely in a vertical plane under
the force of gravity. Let L

be the distance from the pivot point to

the center of mass of the body.

The torque that causes the rotation is produced by the component of
the force of gravity that is perpendicular to the line that joins the
pivot point to the center of mass, mg sin

. The torque is the product

of the lever arm, L

, and the perpendicular force, or

 = L

mg sin

For small angles, sin  = , so the expression for

the torque becomes

 = L

or= kwhere k = L

mg.

Since the expression for torque matches the expression for the restor-
ing force, F = -kx, on an object in simple harmonic motion, the period
of oscillation for the physical pendulum can be written as follows:

where I, the moment of inertia (rotational inertia) for the physical
pendulum, replaces M and L

mg replaces k in the equation for the

period of oscillation of a mass on a spring,

Assume that the Balance Arm beam is a rectangular-type rod. For a rod pivoting
around an axis through its center of mass, the moment of inertia around the center
of mass is:

where m is the mass and L is the length of the rod.

What happens if the rod pivots around one end rather than its center of mass? If
the rod pivots around any other axis that is parallel to the axis through the center of mass, you can use the Parallel
Axis Theorem to calculate the moment of inertia around that parallel axis. The moment of inertia about the parallel
axis, I

parallel

, is the sum of the moment of inertia around the center of mass, I

, plus mL

, where m is the mass

of the rod and L

is the perpendicular distance from the center of mass to the pivot point, or

The formula for the period of oscillation becomes

Item

Statics Board

Balance Arm

Stopwatch (ME-1234)

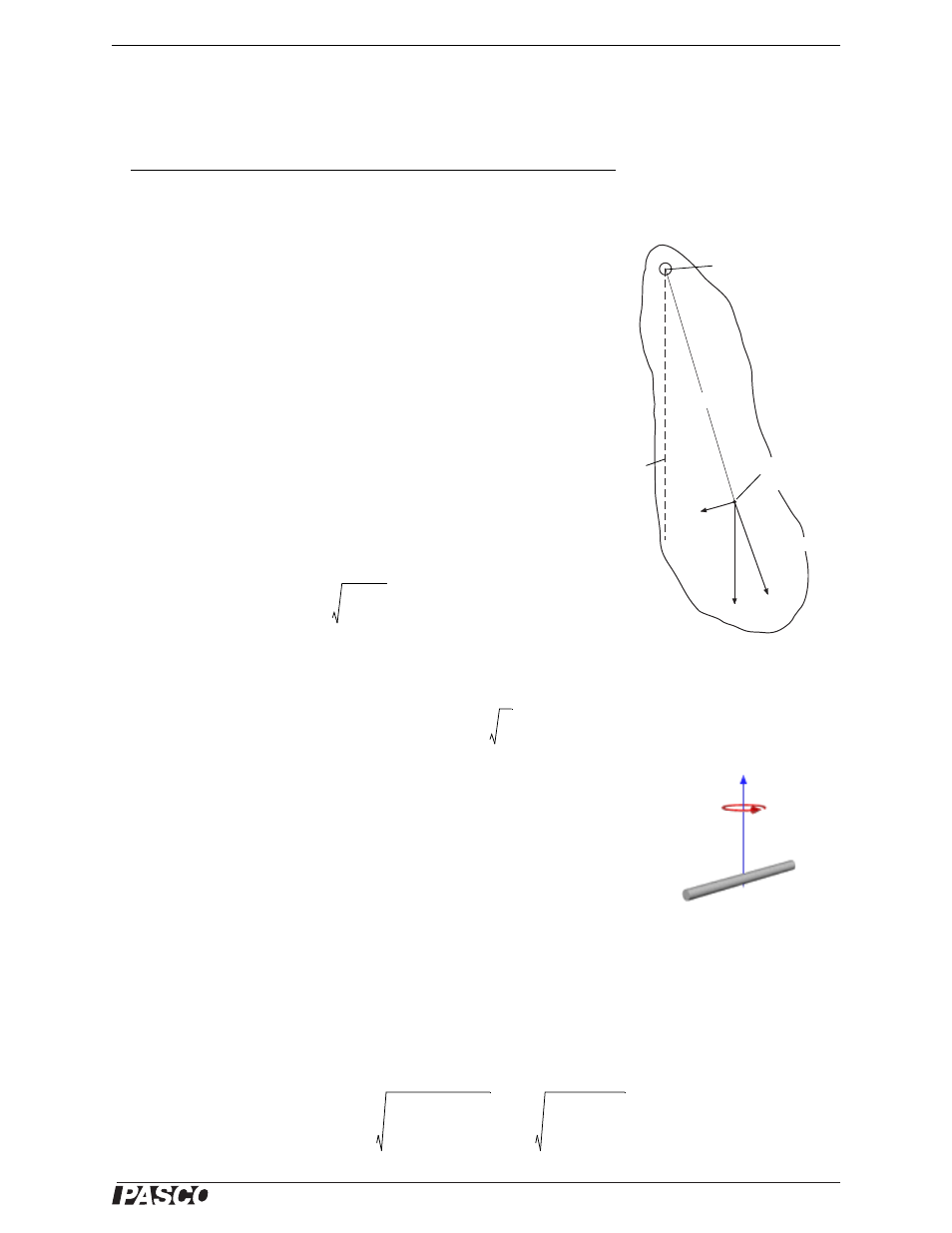
Figure 11.1: Physical Pendulum



mg sin



mg cos



Equilibrium

position

Pivot
point

Center of

mass



-----------------

 M

-----

Fig. 11.2: Moment of Inertia

------mL

parallel

------mL



------mL

----------------------------------------



------L

-------------------------------