Theory – PASCO ME-9502 Statics System User Manual

Page 57

M o d e l N o . M E - 9 5 0 2

E x p . 1 0 : S i m p l e H a r m o n i c M o t i o n – T h e S i m p l e P e n d u l u m

0 1 2 - 1 2 8 7 6 B

Exp. 10: Simple Harmonic Motion–The Simple Pendulum

Equipment Needed

Theory

Simple harmonic motion is not limited to masses on springs.
In fact, it is one of the most common and important types of
motion found in nature. From the vibrations of atoms to the
vibrations of airplane wings, simple harmonic motion plays an
important role in many physical phenomena.

A swinging pendulum, for example, shows behavior that is
very similar to that of a mass on a spring. By making compar-
isons between these two phenomena, some predictions can be
made about the period of oscillation for a pendulum.

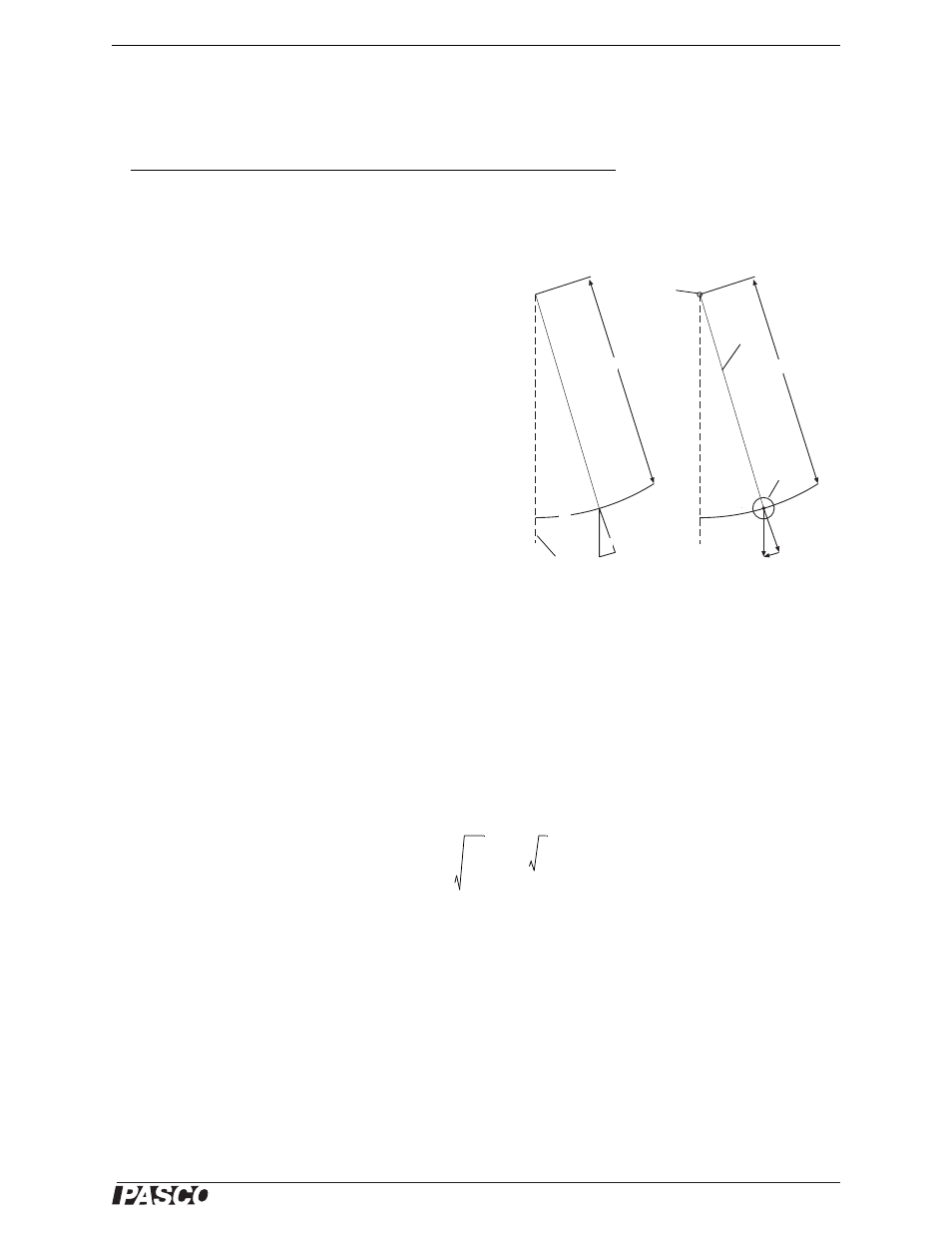
The figure shows a simple pendulum with a string and a mass
at an angle

 from the vertical position. Two forces act on the

mass: the force of the string, T, and the force of gravity. The
gravitational force, F = mg, can be resolved into two compo-
nents. One component, F

radial

, is along the string. The other

component, F

tangential

, is perpendicular to the string and tan-

gent to the arc of the mass as it swings. The radial component of the weight, mg cos

, equals the force, T, through

the string. The tangential component of the weight, mg sin

, is in the direction of motion and accelerates or decel-

erates the mass.

Using the congruent triangles in the figure, it can be seen that the displacement of the mass from the equilibrium
position is an arc whose length, x, is approximately L tan

. If the angle, , is relatively small (less than 20°), then

it is very nearly true that sin

 = tan . Therefore, for small swings of the pendulum, it is approximately true that

tangential

= mg tan

 = mg x/L. Since the tangential force is a restoring force, the equation should be

tangential

= - mg x/L. Comparing this equation to the equation for the restoring force of a mass on a spring,

F = -kx, it can be seen that the quantity mg/L has the same mathematical role as k, the spring constant. On the
basis of this similarity, you can say that the period of oscillation for a pendulum is as follows:

where m is the mass, g is the acceleration due to gravity, and L is the length of the pendulum from the pivot point
to the center of mass of the hanging mass.

In this part of the experiment you will investigate this equation for the period of the simple harmonic motion of a
pendulum.

Item

Statics Board

Utility Mount and Cord Clip

Thread

Mass and Hanger Set

Stopwatch (ME-1234)

Figure 10.1: Pendulum



radial

tangential

mg sin



mg cos



Equilibrium

position

Pivot
point

Mass

String

 m

-------

 L

---