PASCO ME-9502 Statics System - Manual (Page 54)

S t a t i c s S y s t e m S i m p l e H a r m o n i c M o t i o n – B e a m o n a S p r i n g
®
50 012-12876B
Simple Harmonic Motion–Beam on a Spring
Imagine a horizontal beam that is supported by a hinge at one
end and a vertical spring at the other end. If the end of the
beam is pulled down, the spring exerts a restoring force,
F = -kx, to return the beam to its equilibrium position. The
beam will oscillate up and down with a period, T
beam
. For a
mass on a spring, the period, T, is as follows:
where M is the total oscillating mass and k is the spring constant. What is the period for a beam on a spring?
The beam rotates about the hinge as the end attached to the spring oscillates. The force of the spring on the oscil-
lating end of the beam, F = -kx, produces a torque on the beam. Let L be the length of the lever arm of the beam.
The torque due to the spring is
= FL. A net torque causes angular acceleration, , that is directly proportional to
the torque,
, and inversely proportional to the rotational inertia, I. That is,0,
or
 = I. Setting the two expressions for torque equal to each other gives FL = I. Assume that the beam is like a
thin rod pivoted around one end. The rotational inertia of the thin rod is I = 1/3 m L
2
where m is the mass of the
beam. Since the force on the beam is F = -kx, the equation FL =
I becomes:
The angular acceleration,
, and the tangential (linear) acceleration, a
T
, of the oscillating end of the beam are
related. The tangential acceleration, a
T
=
r where r is the radius of rotation. In this case, the radius of rotation is
the lever arm, L, so a
T
=
L, or  = a
T
/L. The expression becomes:
which simplifies to
Solving for the tangential acceleration gives:
The tangential acceleration, a
T
= -
 2
x, so the expression becomes:
Since the angular frequency,
 = 2/T, the period, T = 2/or
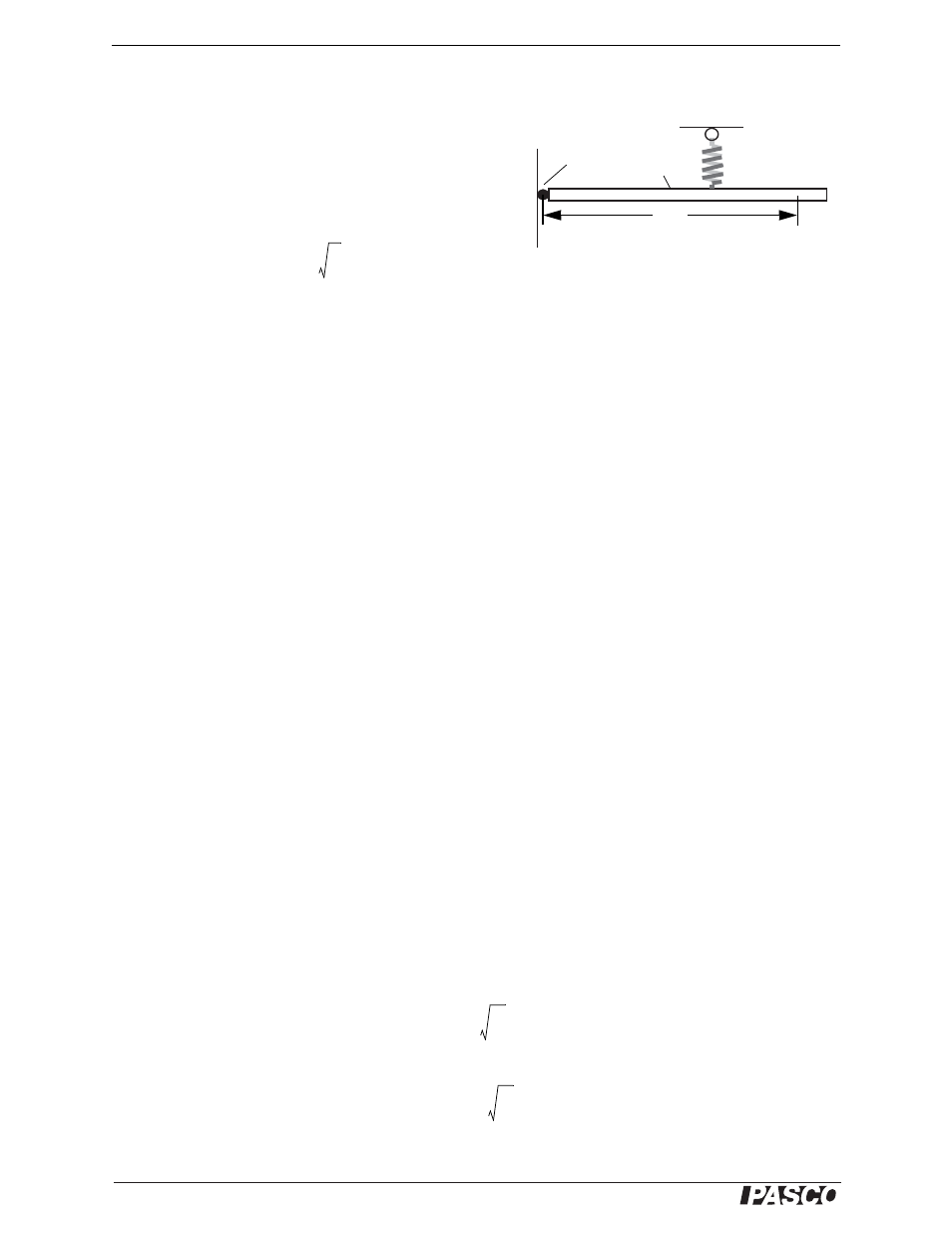
Hinge
Beam
Spring
L
Figure 9.3: Beam on a String
T
M
k
----- =


I
-- =
kxL –
mL 2
3
-------------- =
kxL –
a
T
mL
2
3L
---------------- =
kx –
a
T
m
3
---------- =
a
T
3k
m
------x – =
 2
x –
3k
m
------x – =
 2 3k
m
------ =
 3k
m
------ =
T 2
 m
3k
------ =