Rainbow Electronics ATA5812 - Manual (Page 52)

52
ATA5811/ATA5812 [Preliminary]
4689B–RKE–04/04
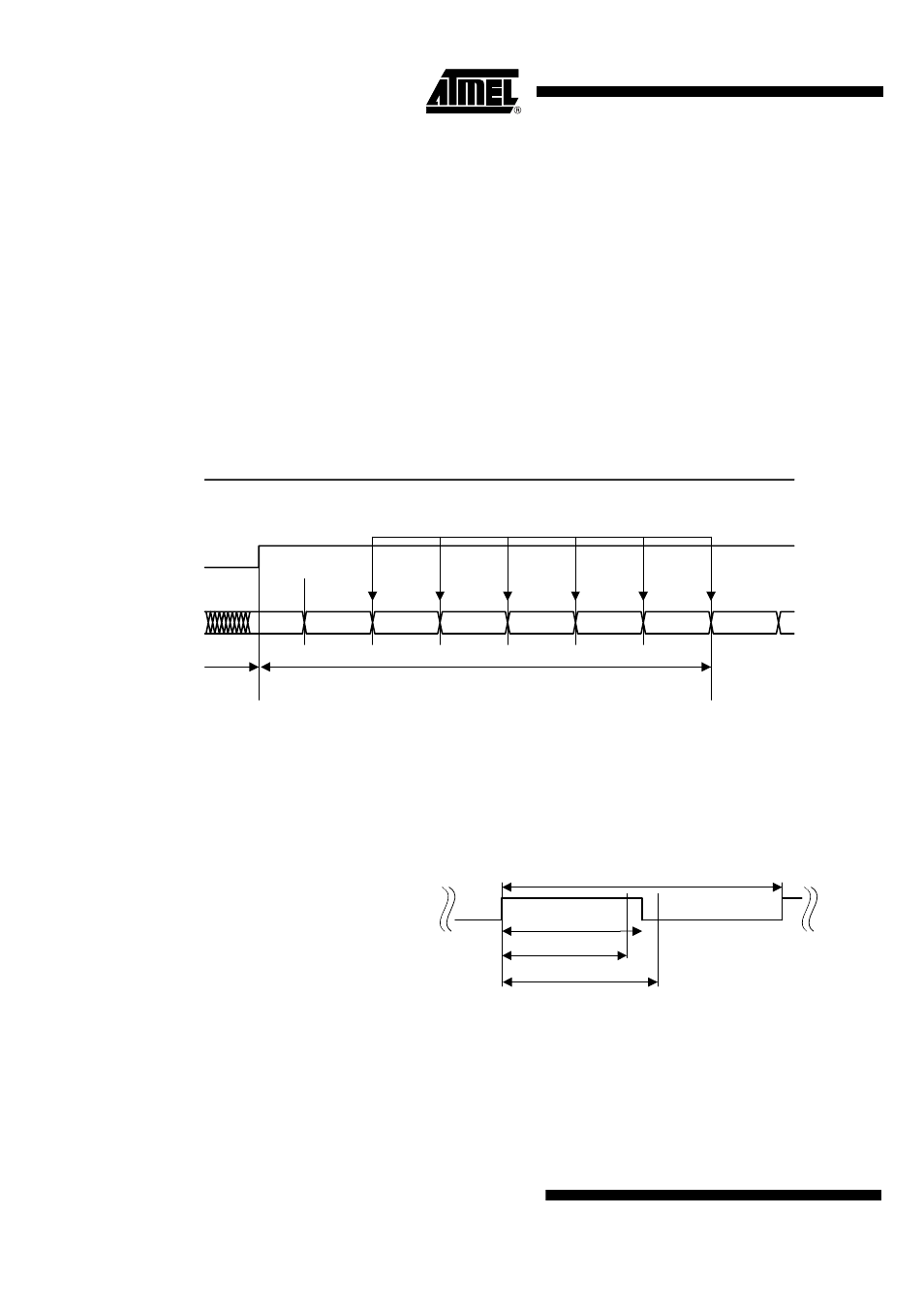
Bit-check Mode In Bit-check mode the incoming data stream is examined to distinguish between a valid
signal from a corresponding transmitter and signals due to noise. This is done by subse-
quent time frame checks where the distance between 2 signal edges are continuously
compared to a programmable time window. The maximum count of this edge to edge
test before the transceiver switches to receiving mode is also programmable.
Configuration the Bit-check Assuming a modulation scheme that contains 2 edges per bit, two time frame checks
are verifying one bit. This is valid for Manchester, Bi-phase and most other modulation
schemes. The maximum count of bits to be checked can be set to 0, 3, 6 or 9 bits via the
variable N
Bit-check
in control register 5. This implies 0, 6, 12 and 18 edge to edge checks
respectively. If N
Bit-check
is set to a higher value, the transceiver is less likely to switch to
receiving mode due to noise. In the presence of a valid transmitter signal, the Bit-check
takes less time if N
Bit-check
is set to a lower value. In RX polling mode, the Bit-check time
is not dependent on N
Bit-check
. Figure 42 shows an example where 3 bits are tested
successful.
Figure 42. Timing Diagram for Complete Successful Bit-check (Number of Checked Bits: 3)
According to Figure 43, the time window for the Bit-check is defined by two separate
time limits. If the edge to edge time t
ee
is in between the lower Bit-check limit T
Lim_min
and the upper Bit-check limit T
Lim_max
, the check will be continued. If t
ee
is smaller than
limit T
Lim_min
or exceeds T
Lim_max
, the Bit-check will be terminated and the transceiver
switches to sleep mode.
Figure 43. Valid Time Window for Bit-check
RX_ACTIVE
Bit check
Demod_Out
T
Startup_Sig_Proc
1/2 Bit
Bit check ok
T
Bit-check
Start-up mode Bit-check mode
1/2 Bit 1/2 Bit 1/2 Bit 1/2 Bit 1/2 Bit
Receiving mode
Demod_Out
t
ee
T
Lim_min
1/f
Sig
T
Lim_max