Kipp&Zonen BSRN Scientific Solar Monitoring System - Manual (Page 147)

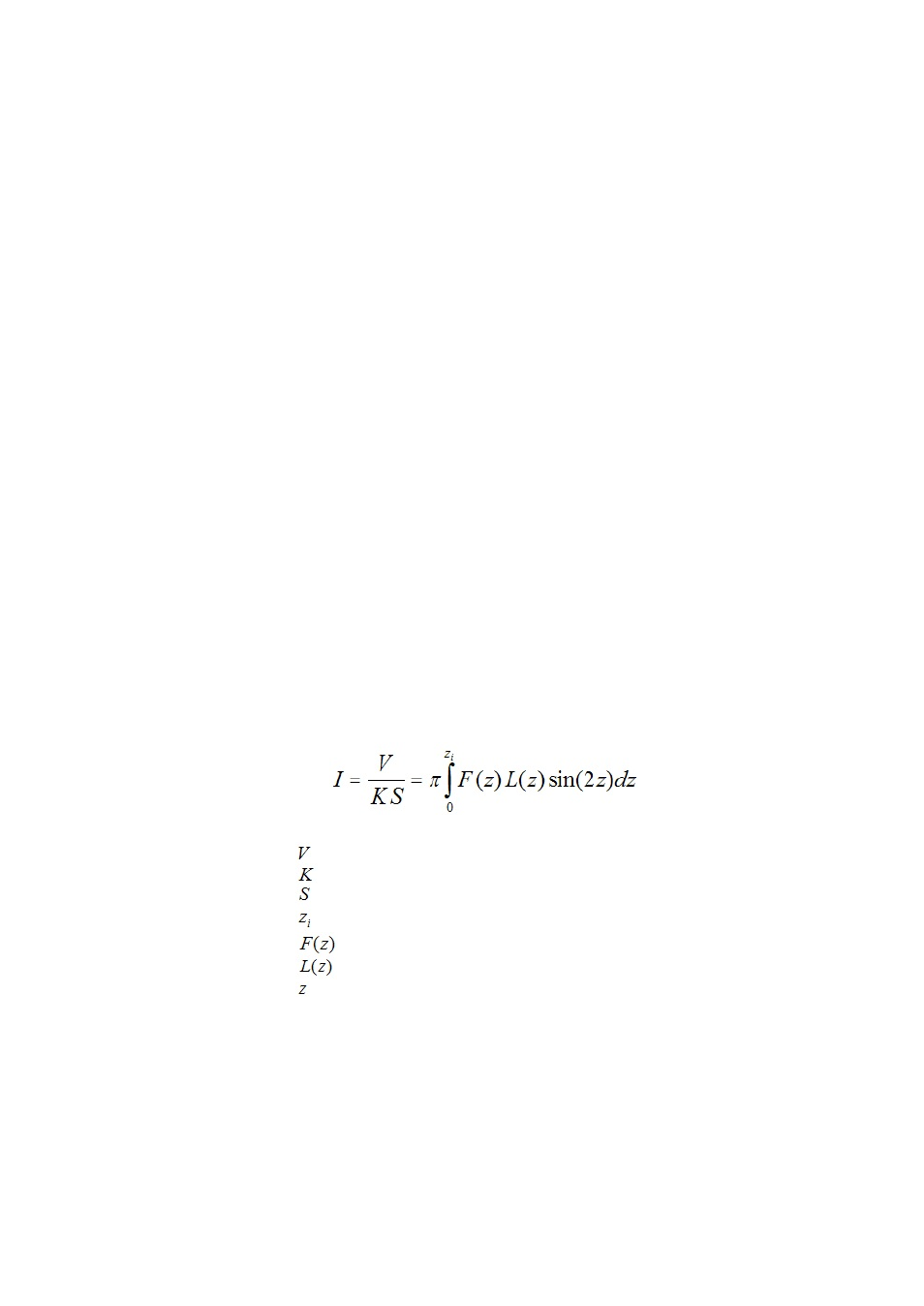
135
Annex D Pyrheliometers and Pointing
D 1. On the Pointing Error of Pyrheliometers
Prepared by G. Major for the BSRN discussion held in Davos, Switzerland, in October of 1995
D 1.1 Introduction
The direct radiation is the solar radiation com ing from the solid angle determ ined by the solar disk.
The pyrheliom eters are designed to m easure the direct radiation. T heir view lim iting angles (slope,
opening and lim it angle) are larger than the visible radius of the solar disk. This is partly due for the
easier tracking of the Sun: if the lim iting angles are larger than the solar disk, it is not necessary to
follow the Sun quite precisely.
How large pointing errors or inaccuracies occur in the everyday practice? Let us take a hand-operated
pyrheliom eter. If its adjustm ents are m ade once in a m inute, its largest m ispointing in azim uth angle
would be one quarter of a degree. The deviation from the right position in elevation angle is in the sam e
order. Regarding the pointing devices of the pyrheliom eters, 1 m m deviation of the illum inated spot
from its proper position could be regarded as large m ispointing. Depending on the length of the pointing
path, this deviation m eans about half a degree of pointing error.
The purpose of this docum ent is to present calculated values of the errors in the output of pyrheliom eters
caused by pointing uncertainty up to 2 degrees. Two atm ospheric conditions are taken into account:
-- m ountain aerosol, optical depth: 0.07, solar elevation: 60 degrees, direct radiation: 1000 W m ; -2
-- continental background aerosol, optical depth: 0.23, solar elevation: 20 degrees, direct radiation:
461 W m .
-2
The calculations have been m ade for 3 pyrheliom eters: the PacRad size cavity instrum ent (ABS), the
KIPP and NIP pyrheliom eters. Their slope angles are: 0.75, 1.0 and 1.78 degrees respectively.
D 1.2 The method of calculation
The calculation is based on the Pastiels` theory (see for exam ple in Major 1994). The irradiance given
by a circular pyrheliom eter can be written as:
where = the output of the pyrheliom eter,
= the average sensitivity of the receiver,
= the area of the receiver,
= the lim it angle of the pyrheliom eter,
= the penum bra function of the pyrheliom eter,
= the radiance (=sky function)
= the angle between the direction of radiance and the optical axis of the
pyrheliom eter.
Circular pyrheliom eter m eans that all the view lim iting diaphragm s and the receiver are circular in shape,
that is the whole pyrheliom eter has a rotational sym m etry around its optical axis. In the equation the
sam e rotational sym m etry is supposed for the solar disk and the circum solar sky.