Kipp&Zonen BSRN Scientific Solar Monitoring System - Manual (Page 142)

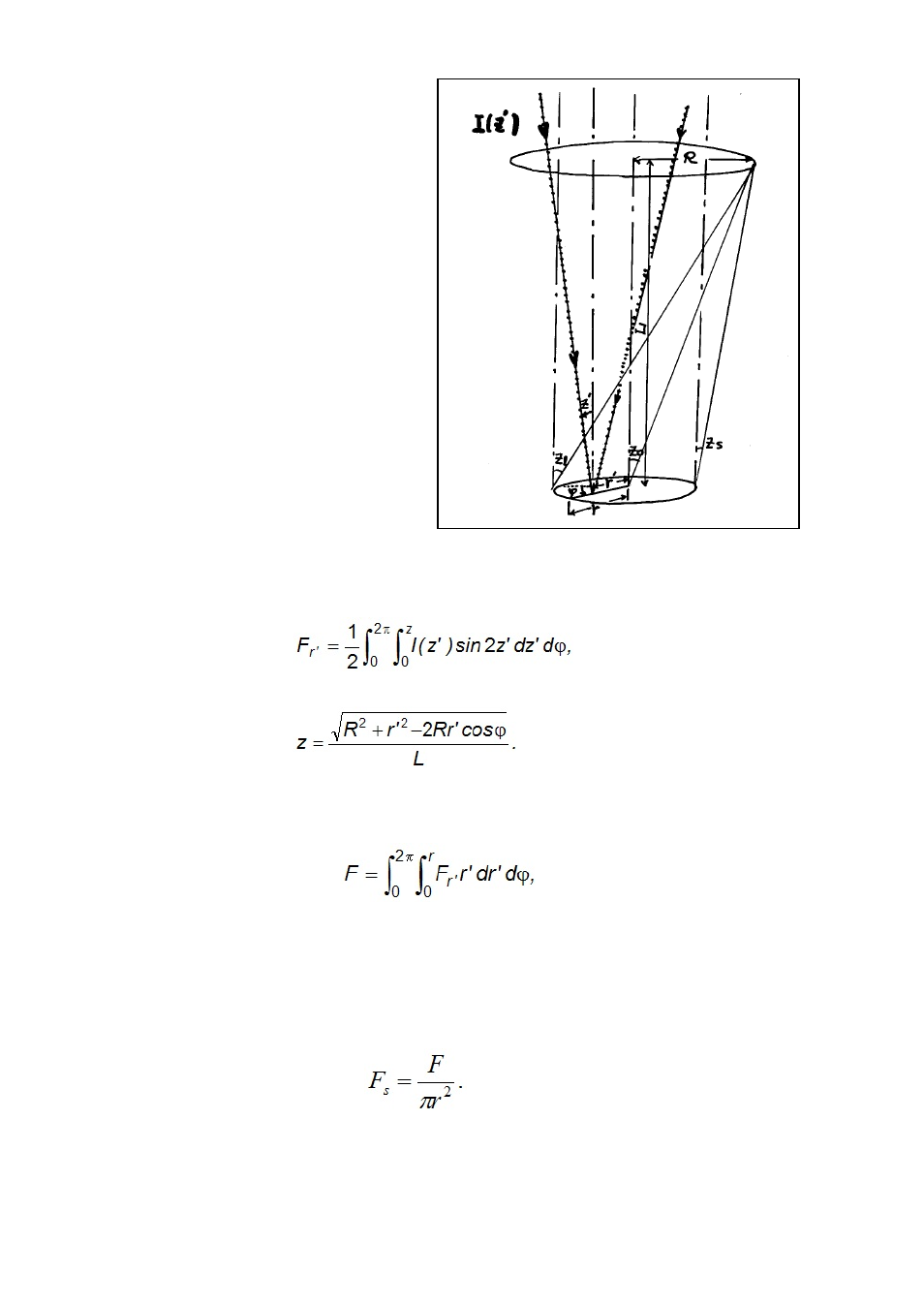
130
Figure C 4.2. Relationship between the geom etry of
pyrheliom eters and radiance (The relationship
applies for a diffusom eter when the sun is at zenith).
C 4.2 Irradiance in the instrument: Numerical
solutions
Since the relationship between the radiation
and the sensor continuously changes with
the solar zenith angle, exact com parability
happens only when the sun is at zenith. This
rare occasion nevertheless is useful to
develop the general case for which m ost
m easurem ents are carried out.
C 4.3 Sun at zenith
The geom etrical condition between radiance
and an instrum ent is illustrated in Figure C
4.2 for the sun at zenith. The sam e figure
represents both pyrheliom eters and
diffusom eters by swiching the frontal circle
between the opening and the shading disc
(or sphere). W e consider a point on the
sensor which is located at a distance of r'
m easured from the sensor centre. Radiance
at this point falls at a zenith angle of z'. W e
r '
consider total irradiance F at this point
com ing into the instrum ent (or blocked by the
shading disc). This calculation involves a
double integration, one from the norm al to
the sensor to the edge of the opening (or disc)
whose angle to the norm al is z, the other from
0º to 360º in azim uth:
where
r'
This irradiance F expected at r' on the sensor m ust be integrated for the entire sensor surface to
obtain the absolute am ount of radiative flux (or the am ount blocked by the shading disc):
where r = the radius of the sensor.
This radiative flux can be converted for a unit area to obtain the irradiance expressed in the
conventional unit.