Ocean Optics ElliCalc - Manual (Page 52)

Ocean Optics Germany GmbH Thin Film Metrology
51
9.2 Main menu “Options”
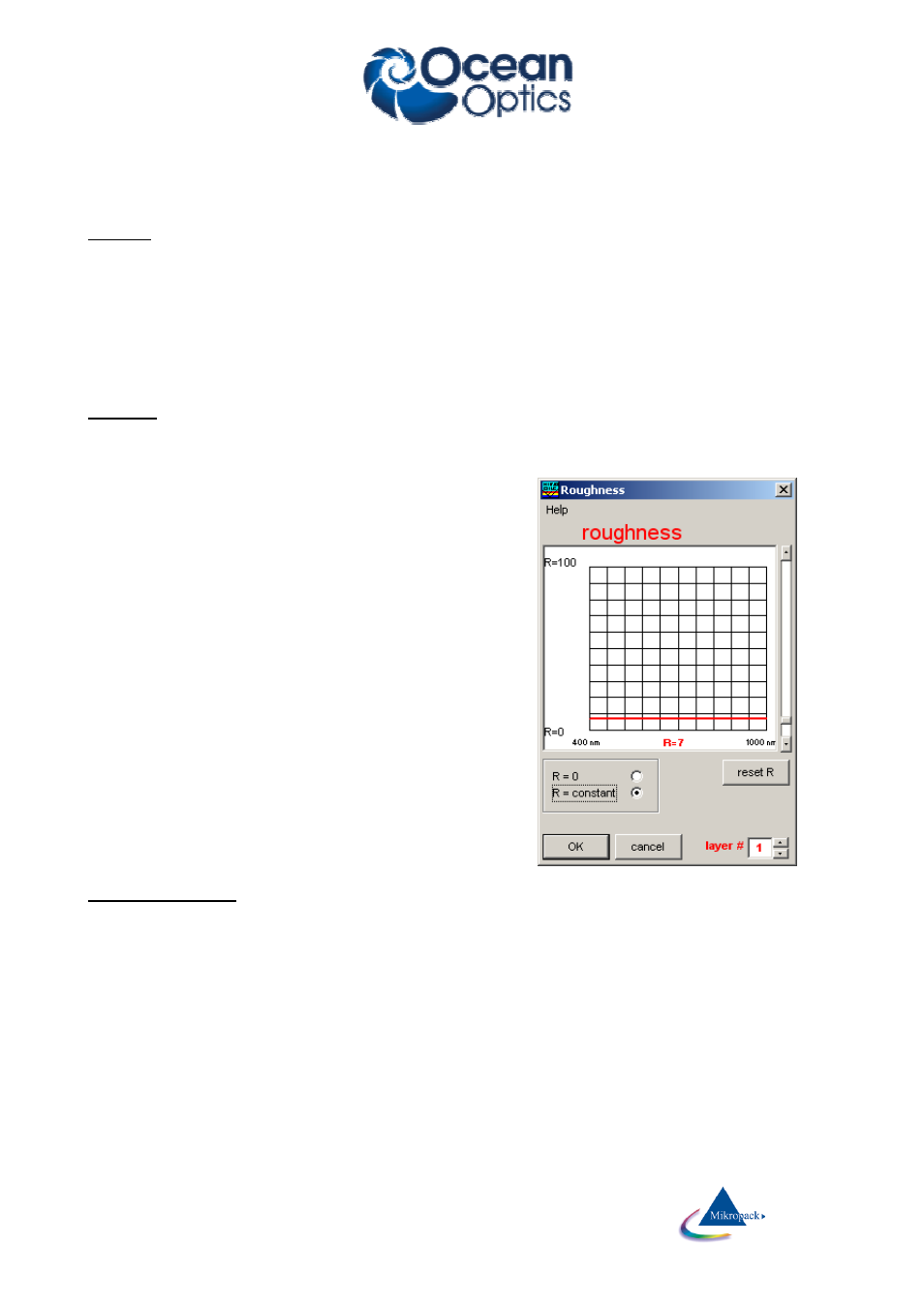
9.2.1 Roughness
General:
It is quite difficult to measure interference if the substrate or the layers are rough, as the interference
patterns get lost.
Example: Roughness is quite common for thick layers like 20 micrometers of photoresist, as the drying
process is very critical and the shrinking of the resist does not lead to perfect surfaces.
Roughness is also quite common for technical surfaces like aluminum or brass or steel that are to be
covered with protection layers (like DLC=diamond like carbon layers).
Methods:
In ElliCalc internal mode (not in SCOUT mode!) an empirical method is implemented to deal with
roughness:
1. no roughness
No roughness is included in the calculation (=default).
2. constant roughness
You will see some textboxes in the setup area which show
“R-factors” for each interface. This value means a
percentage of light that is regarded as lost at this interface.
So there is no real physical roughness model. Such a
physical model cannot be given as the typical size of the
roughness is absolutely unknown. This means that even the
scattering mechanism (Mie scattering, Rayleigh scattering
etc) is unknown. There are some formulae in the literature
but in our case these are not better than the above
mentioned method of light loss via some empirical R-
Factors.
An R-factor of R=0 means a perfect surface = no roughness
An R-factor of R=50 means a loss of 50% light at this
interface.
There is no wavelength dependency of these empirical
factors.
In
the current version there is no wavelength dependency of
these empirical factors.
constant roughness
Attention:
You have to input roughness values in the setup roughness textboxes.
At each interface a certain amount of light is regarded as lost. This percentage has to be input via
roughness textboxes in the setup area. These R-factors are not dependent on wavelength.
This algorithm does NOT manipulate measured data, but the measured amplitude might still differ
considerably from the simulated amplitudes. This means that the fit procedure might still have problems to
find a good solution.