Appendix d current regulation using pid techniques – High Country Tek emc-3L User Manual
Page 96
14 Appendix D
Current Regulation using PID techniques
PID, proportional integral differential control, is a powerful and popular method of regulating systems. Typical
applications include speed control and position control. HCT uses PID to control a proportional valve’s
performance to compensate for the variations in system parameters such as the wire lengths and other
resistance sources that can affect the positioning of a valve.
It will be easier to tune your system’s valves using a PID loop if you understand the basic concepts first.
This is intended to be a brief over view of a very complicated subject. See HCT manuals for more details on how
to tune our products.
The spool in a proportional valve moves due to the magnetic field that is created by the current through the
valve’s coil. The amount of coil current is proportional to the supply voltage applied to the high-side coil contact,
the amount of time (duty cycle) that the current is allowed to flow through the coil by the opening and closing of
a switch on the low-side of the coil and the total resistance in the complete current path to and from the coil.
PID is a method by which the duty cycle of the applied current is varied to achieve the desired current through
the coil given all of the system wiring variations. PID also provides a means by which this desired current is
reached quickly and accurately. Pulse Width Modulation (PWM) is term used for the amount of time current is
allowed to flow through the coil. PID increases or decreases the PWM percentage according to the error seen
in the measured current through the coil versus the desired current.
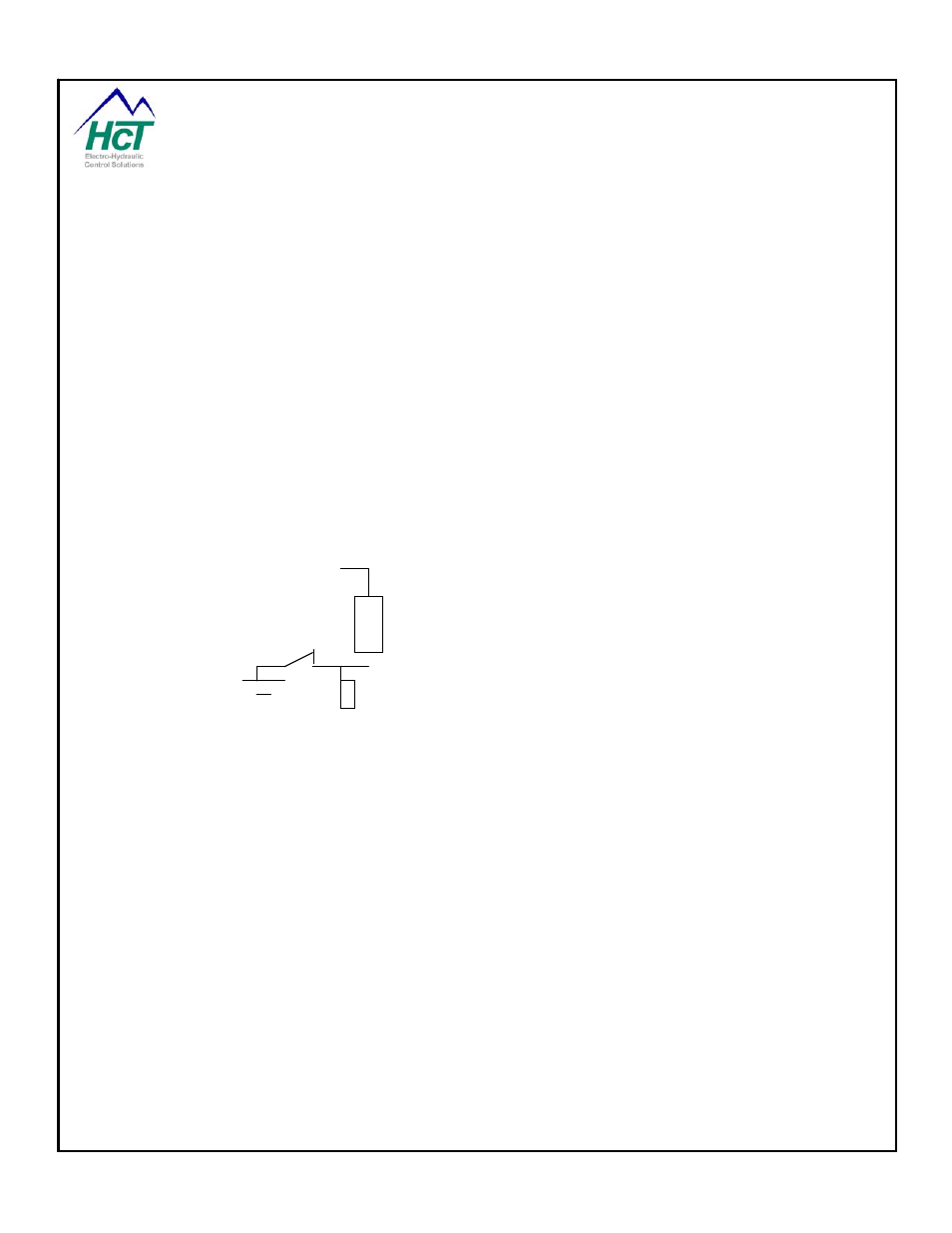
The basic proportional valve control circuit looks like the following:
High-Side
Voltage source
Valve
(Spool)
Positioning
Coil
Switch
Low-Side Input
Programmable
Switch (PWM)
Current Measuring Device
GND
Ideally closed loop control (like PID) of systems is used to cause the system/valve to arrive at a commanded
state (i.e. valve fluid flow) exactly. This form of control automatically adjusts out many non-ideal characteristics
of your system and is perform on each proportional valve individually. To have this level of control there must be
feedback from the system to tell the closed loop controller where the system is so that it will know when it has
arrived at the desired state. First, there must be a command from the user (current or fluid flow value) to tell the
controller where the system should be. When the feedback (current or actual fluid flow) differs from the
command there is an error. So just correct it right? The problem is inertia, inductance and delay in the system,
sensors and electronics. These effects can cause over correction by the controller. For example if you try to
point a satellite mini dish by having someone yell STOP when the signal is good, you will generally over shoot
the optimum position given the time it takes the person to react to observing the good signal. Over shoot is
going past the desired setting because of a delay in getting the feedback, or a delay in stopping the change in
the system. If you see that you have gone past the commanded system state and then reverse the movement to
compensate, you can then over shoot in the opposite direction. Multiple over shoots are called oscillation. One
solution to the delay problem is to slow down the system's rate of change so much that the delays and inertia
are insignificant. This is usually not a good solution, as most designers want a quick and controlled response
from the machine.
How the system responds to the error is tunable by setting the PID parameters (2-3 numeric constants typically
set to 10 for DVC products). These settings will determine the speed of correction, degree of over shoot,
maximum error and final error. The settings are termed the proportional, integral and differential settings. They
are used in combination to determine the PWM% change each timing cycle. The proportional term as its name
implies will drive the output proportional to the error (set the PWM %), causing the system to change more
rapidly as the error increases. As the error approaches zero, the proportional term also approaches zero and will
+V
P/N: 021-00163, Rev. A.0 - for V5.2 Tools
Page | 96
