HP 39g Graphing Calculator - Manual (Page 188)

Reduced-Row
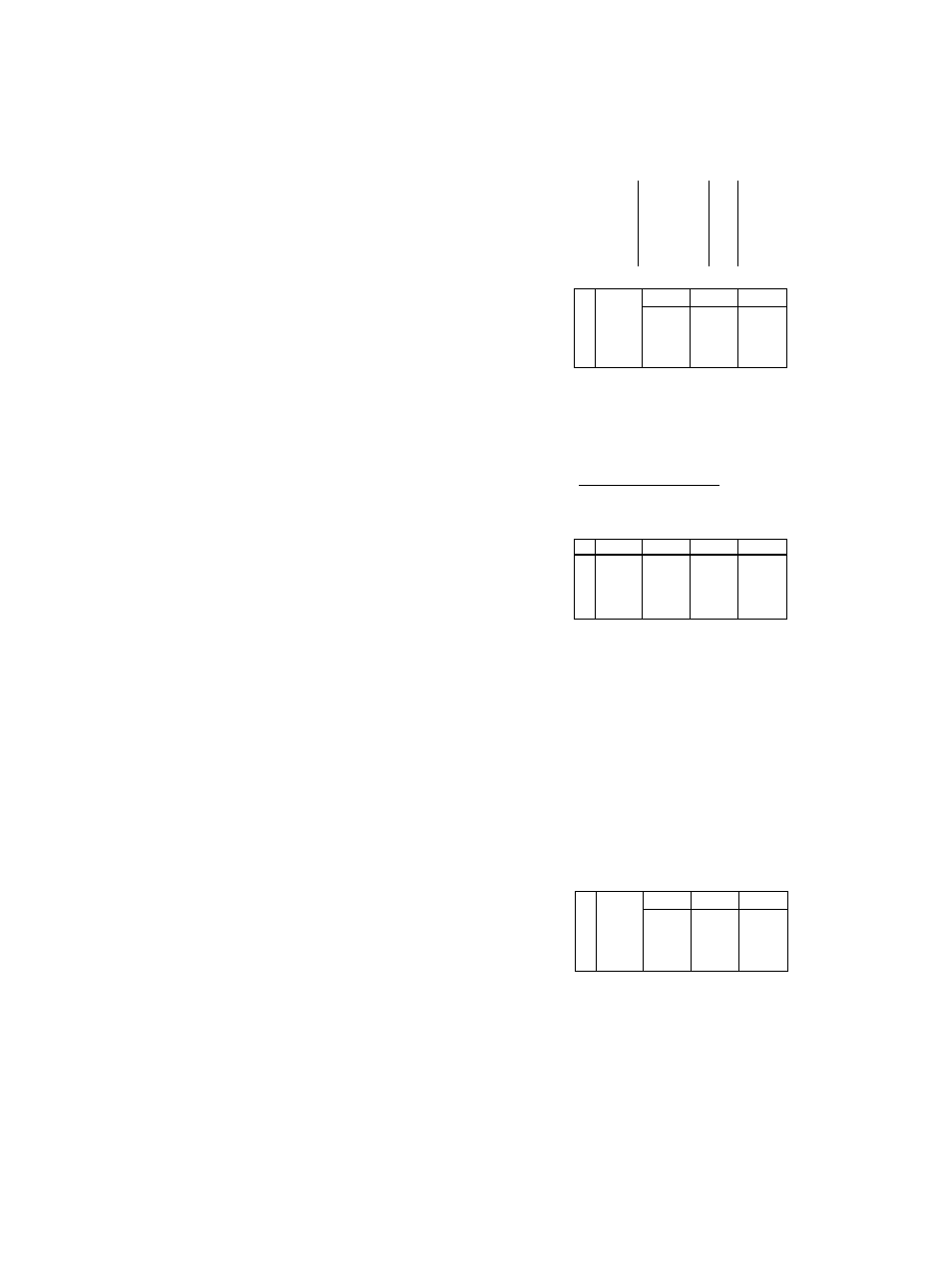
Echelon Form The following set of equations x ~ 2 y + 3 z = 14
2 x + y - z = ^3
4 x - 2 y + 2 z = 14
can be written as the augmented matrix
which can then stored as a
3x4 real matrix in Ml.
1 -2 3 14
2 1 - 1
-3
4 -2 2 14_
Ml 11 2 3 4
1 -s 3 IH
1
-1
-3
d H -s s
IH
You can use the RREF
function to change this to
reduced row echelon form,
storing it as M2 for
convenience.
The reduced row echelon
matrix gives the solution to
the linear equation in the
forth column.
RREF Oil >W2
[[1,0,8, n,C0,l»0!-23.
Ma 1 2 3 4
1 1
0
0 1
? (1 1 0 -a
d 0 1 3
An advantage of using the RREF function is that it will also
work with inconsistent matrices resulting from systems of
equations which have no solution or infinite solutions.
For example, the following set of equations has an infinite
number of solutions:
A' + y - z = 5
2.t--v = 7
x ^ 2 y + z = 2
The final row of zeros in the
reduced-row echelon fonn of
the augmented matrix
indicates an inconsistency.
ME 1 2 3 4
1 0 -.333334
F 1 -.SÉÉ6?
1
3 0 0 0
12-14 Matrices