Altera FFT MegaCore Function User Manual
Page 48
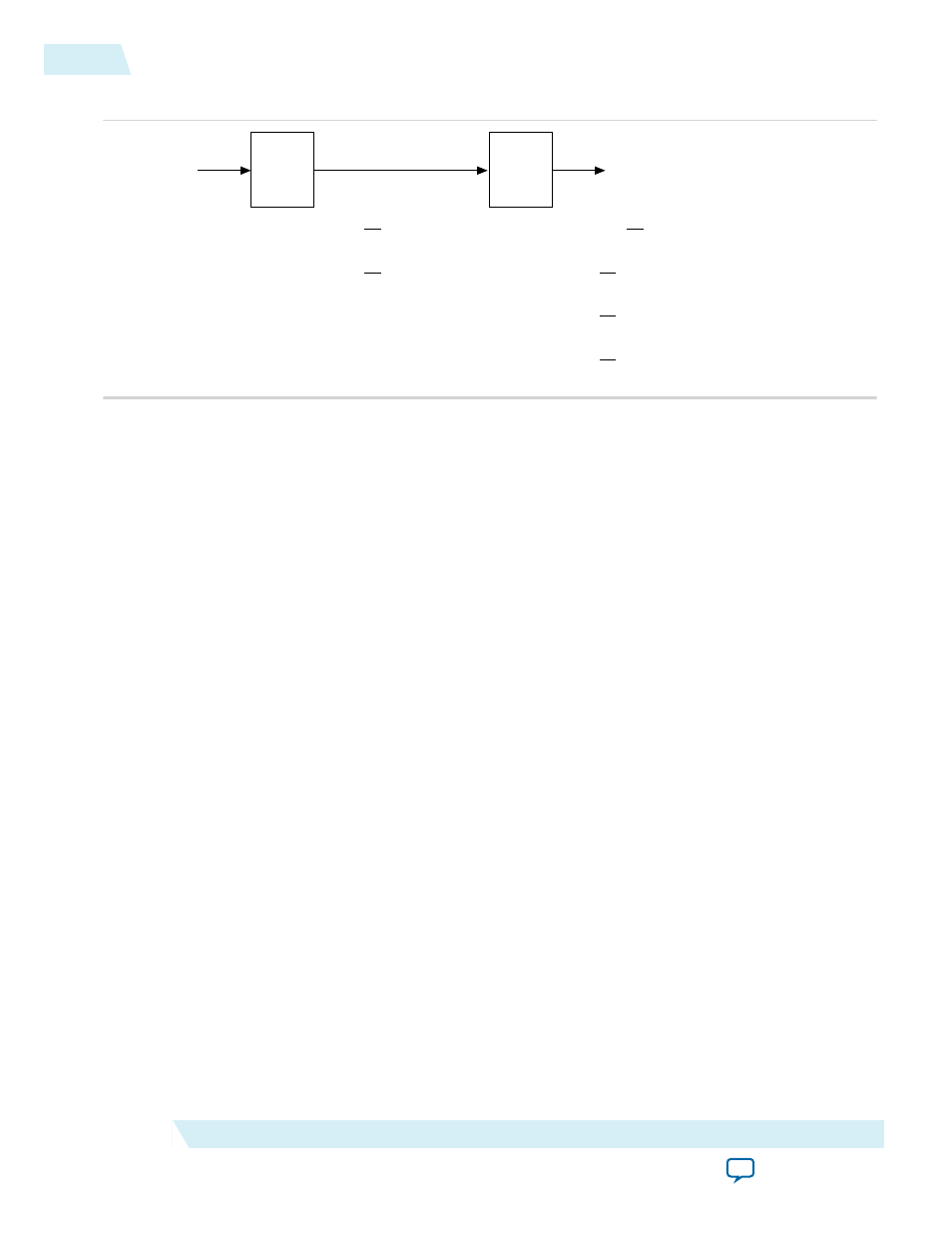
Figure 4-2: Derivation to Achieve IFFT/FFT Pair Unity Gain
IFFT
x0
X0 = IFFT(x0)
=
N
1
× IFFTa (x0)
=
N
1
× data1 × 2 –exp1
FFT
x0 = FFT(X0)
= FFT(
N
1
× data1 × 2 –exp1)
=
N
1
× 2–exp1 × FFTa (data1)
=
N
1
× 2–exp1 × data2 × 2 –exp2
=
N
1
× 2
–exp2
–exp1
× data2
where:
x0 = Input data to IFFT
X0 = Output data from IFFT
N = number of points
data1 = IFFT output data and FFT input data
data2 = FFT output data
exp1 = IFFT output exponent
exp2 = FFT output exponent
IFFTa = IFFT
FFTa = FFT
Any scaling operation on X0 followed by truncation loses the value of exp1 and does not result in unity
gain at x0. Any scaling operation must be done on X0 only when it is the final result. If the intermediate
result X0 is first padded with exp1 number of zeros and then truncated or if the data bits of X0 are
truncated, the scaling information is lost.
One way to keep unity gain is by passing the exp1 value to the output of the FFT block. The other way is
to preserve the full precision of data1×2
–
exp1 and use this value as input to the FFT block. The
disadvantage of the second method is a large size requirement for the FFT to accept the input with
growing bit width from IFFT operations. The resolution required to accommodate this bit width will, in
most cases, exceed the maximum data width supported by the core.
RL** For more information, refer to the Achieving Unity Gain in Block Floating Point IFFT+FFT Pair
design example under DSP Design Examples at
.
Related Information
For more information
4-6
Unity Gain in an IFFT+FFT Pair
UG-FFT
2014.12.15
Altera Corporation
Block Floating Point Scaling
