2corrections at high pressure – Vaisala HMP260 User Manual

Page 115

HMP260 SERIES
Appendix 6: Calculation formulas

HMP260-U017en-1.5

CORRECTIONS AT HIGH PRESSURE

The saturation pressure of water vapour calculated with equation (4) is accurate only in
vacuum where water vapour is the only gas present. In presence of other gases the real
saturation pressure of water vapour P

will rise. At pressure levels up to the normal

atmospheric pressure this effect causes only a minimal error in the calculated variables
and can therefore be ignored. However, at ambient pressures significantly above normal
atmospheric pressure corrections should be made. The pressure correction of P

not included in the software of HMP260 series and therefore it must be made
separately.

When using the HMP264 at ambient pressures significantly above normal atmospheric
pressure, an enhancement factor f can be used to correct P

. The enhancement factors

listed in the table below have been proposed for CO

-free air

at different

temperatures and pressures. The corrected partial pressure of saturated water vapour is
then

ws corrected

⋅

(5)

With the help of the corrected water vapour pressure more accurate calculatios of the
dewpoint temperature, mixing ratio and absolute humidity are possible.

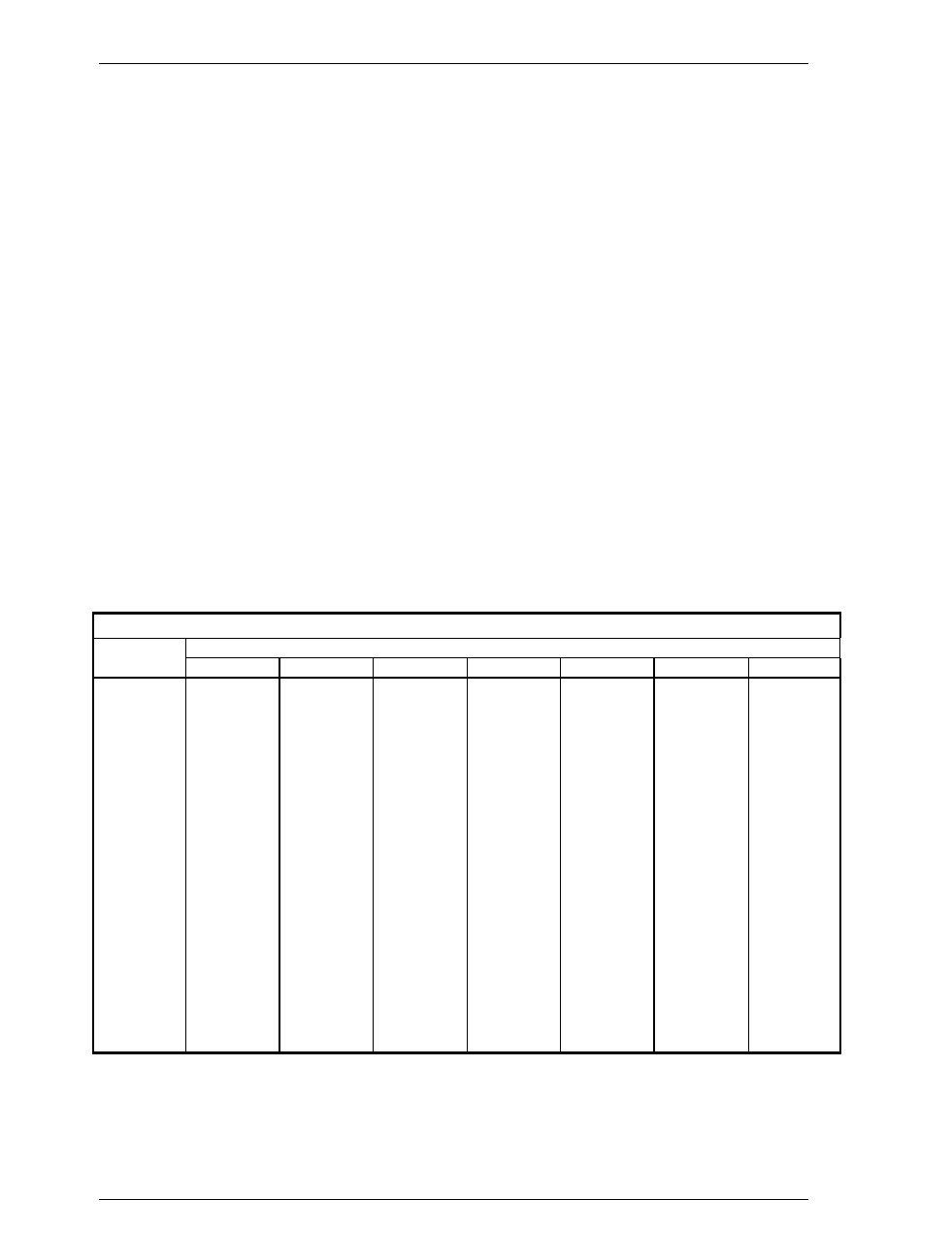
Enhancement factors f

Total press.

t (°C)

(bar)

-40

-20

0.25

1.0013

1.0012

1.00131

1.00173

1.00223

1.00111

1.00

1.0052

1.0044

1.0039

1.00400

1.00467

1.00571

1.00564

2.00

1.0104

1.0086

1.0074

1.0069

1.00728

1.00839

1.00968

3.00

1.0156

1.0129

1.0108

1.0099

1.0098

1.0108

1.01234

4.00

1.0209

1.0172

1.0144

1.0128

1.0124

1.0130

1.0146

5.00

1.0262

1.0215

1.0179

1.0158

1.0149

1.0153

1.0168

10.00

1.0533

1.0435

1.0356

1.0308

1.0277

1.0265

1.0271

20.00

1.110

1.089

1.072

1.0615

1.0539

1.0493

1.0474

30.00

1.171

1.138

1.111

1.093

1.081

1.073

1.0680

40.00

1.237

1.189

1.151

1.126

1.109

1.096

1.0890

50.00

1.307

1.243

1.193

1.161

1.137

1.121

1.111

60.00

1.38

1.300

1.237

1.196

1.167

1.146

1.133

70.00

1.46

1.360

1.282

1.233

1.197

1.172

1.155

80.00

1.55

1.42

1.330

1.271

1.228

1.198

1.178

90.00

1.64

1.49

1.381

1.311

1.261

1.226

1.202

100.00

1.75

1.56

1.43

1.352

1.294

1.254

1.226

1) Hyland R.W., Journal of Research of the NBS, Vol. 80A, No. 4 (1975) pp. 551-

559