Casio fx-5800P - Manual (Page 45)

E-44
b
z – {MATH} 1(∫ dX)
iS0(X)),1,1i(%)1))E
A Remarks
• Use of
∫ ( is supported in the COMP, SD, REG, and EQN Modes only.
• The following functions cannot be input for the f ( x ), a , b , and tol parameters:
∫ (, d / dx (,
d 2
/ dx 2
(,
Σ (. In addition, the Pol( and Rec( functions, and the random number functions
cannot be input for the f ( x ) parameter.
• The integration result will be negative when the limit of region of integration parameters
are within the range a < x < b and f ( x ) < 0.
Example:
∫ (0.5X 2
– 2, –2, 2) = –5.333333333
• In the case of integration of a trigonometric function, select Rad for the angle unit.
• Integration calculations can take a long time to complete.
• Specifying a smaller value for the
tol parameter tends to improve precision, but it also
causes the calculation to take more time. Specify a tol value greater than 1 × 10
–14
.
• You will not be able to input a tol value while using natural display.
• The type of function being integrated, positive and negative values within the region of
integration, and the region of integration being used can cause large error in integration
values and errors.
• You can interrupt an ongoing integration calculation operation by pressing o.
A Tips to for Successful Integration Calculations
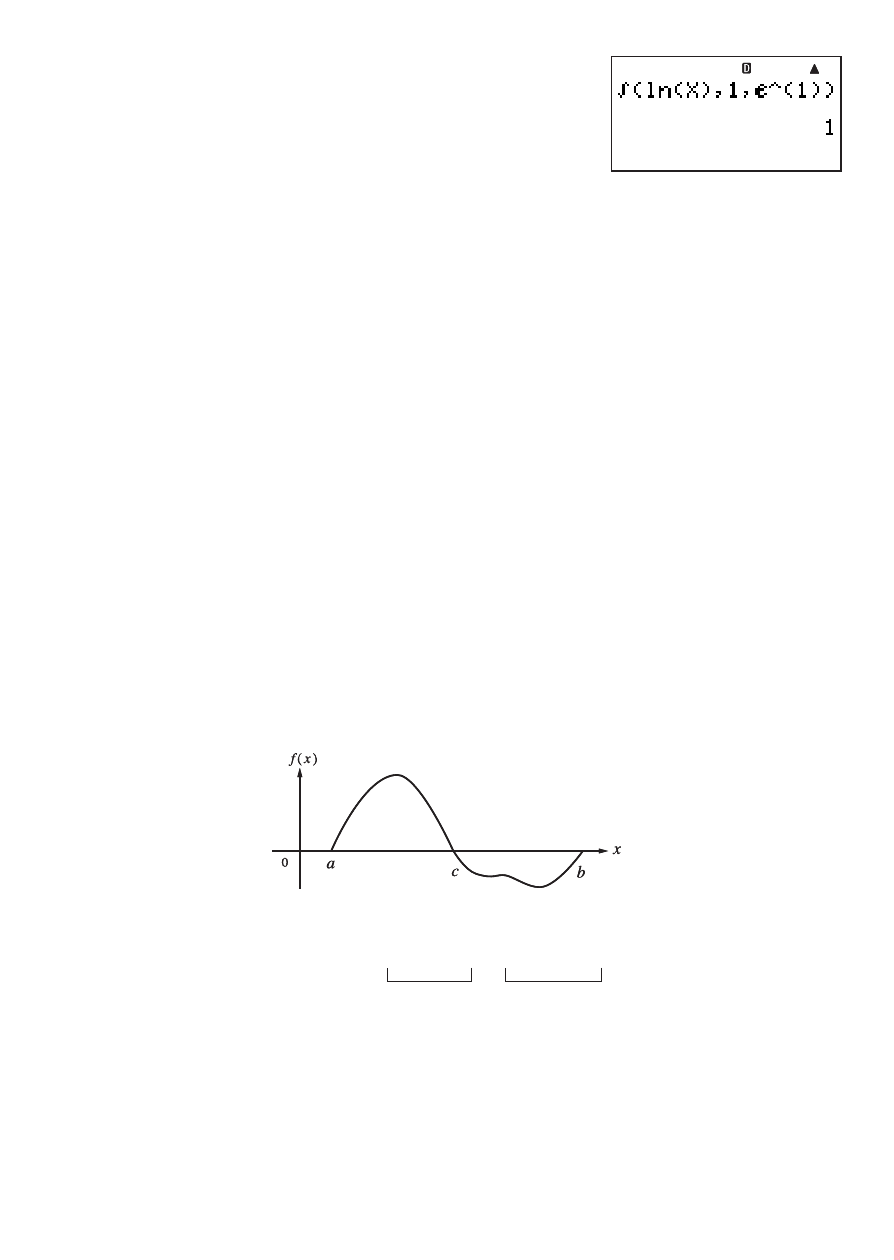
• For periodic functions, and for positive and negative f ( x ) values due to the region of
integration being used
/ Divide the integration into parts for each period, or between positive and negative
parts, obtain integration values for each, and then add the values.
S Positive
S Negative
Positive Part Negative Part
( S Positive) ( S Negative)
• For widely fl uctuating integration values due to a minutely shifting region of integration
/ Divide the integration interval into multiple parts (in a way that breaks areas of wide
fl uctuation into small parts), perform integration on each part, and then combine the
results.
∫ ∫ ∫
a
b
f(x)dx =
a
c
f(x)dx + (–
c
b
f(x)dx)
∫ ∫ ∫
a
b
f(x)dx =
a
c
f(x)dx + (–
c
b
f(x)dx)