Graphing a system of equations in fldoff format – Texas Instruments TI-86 User Manual
Page 154
142
Chapter 10: Differential Equation Graphing
10DIFFEQ.DOC TI-86, Chap 10, US English Bob Fedorisko Revised: 02/13/01 2:28 PM Printed: 02/13/01 3:02 PM Page 142 of 20
10DIFFEQ.DOC TI-86, Chap 10, US English Bob Fedorisko Revised: 02/13/01 2:28 PM Printed: 02/13/01 3:02 PM Page 142 of 20
10DIFFEQ.DOC TI-86, Chap 10, US English Bob Fedorisko Revised: 02/13/01 2:28 PM Printed: 02/13/01 3:02 PM Page 142 of 20
Graphing a System of Equations in FldOff Format
For this example, you must transform the fourth-order differential equation
y
(4)
N
y=e
L
x
into an
equivalent system of first-order differential equations, as shown in the chart below.
Differentiate...
Define the variables as...
And then substitute:
t
=x
Q'1
=y'
Q1
=y
Q'1
=
Q2
(since
Q'1
=y'=
Q2
)
Q'2
=y''
Q2
=y'
Q'2
=
Q3
Q'3
=y'''
Q3
=y''
Q'3
=
Q4
Q'4
=y
(4)
Q4
=y'''
Q'4
=e
Lt
+
Q1
(since
Q'4
=y
(4)
=e
Lx
+y=e
Lt
+
Q1
)
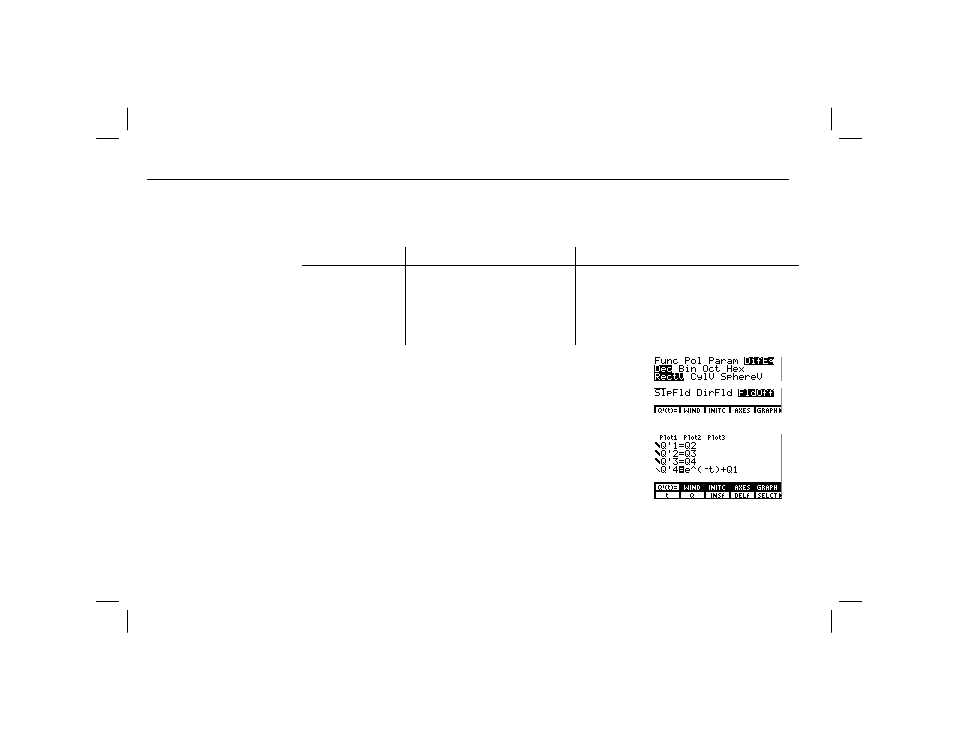
ᕡ Display the mode screen and set
DifEq
graphing mode.
- m # # #
# " " " b
ᕢ Display the format screen and set
FldOff
field format.
6 / & #
# # # # " "
b
ᕣ Display the equation editor and store the
transformed system of differential
equations for y
(4)
=e
Lx
+y, substituting as
shown in the chart.
ᕤ Deselect
Q'3
,
Q'2
, and
Q'1
to plot
Q'4=e^(
L
t)+Q1
only.
& '
2
# '
3
#
'
4
# - ‚ D
a & E \ '
1
$ * $ * $ *
In DifEq graphing mode, t is
the independent variable and
Q'
n
is the equation variable,
where
n
‚
1 and
9.
