Texas Instruments TI-86 - Manual (Page 152)

140
Chapter 10: Differential Equation Graphing
10DIFFEQ.DOC TI-86, Chap 10, US English Bob Fedorisko Revised: 02/13/01 2:28 PM Printed: 02/13/01 3:02 PM Page 140 of 20 10DIFFEQ.DOC TI-86, Chap 10, US English Bob Fedorisko Revised: 02/13/01 2:28 PM Printed: 02/13/01 3:02 PM Page 140 of 20 10DIFFEQ.DOC TI-86, Chap 10, US English Bob Fedorisko Revised: 02/13/01 2:28 PM Printed: 02/13/01 3:02 PM Page 140 of 20
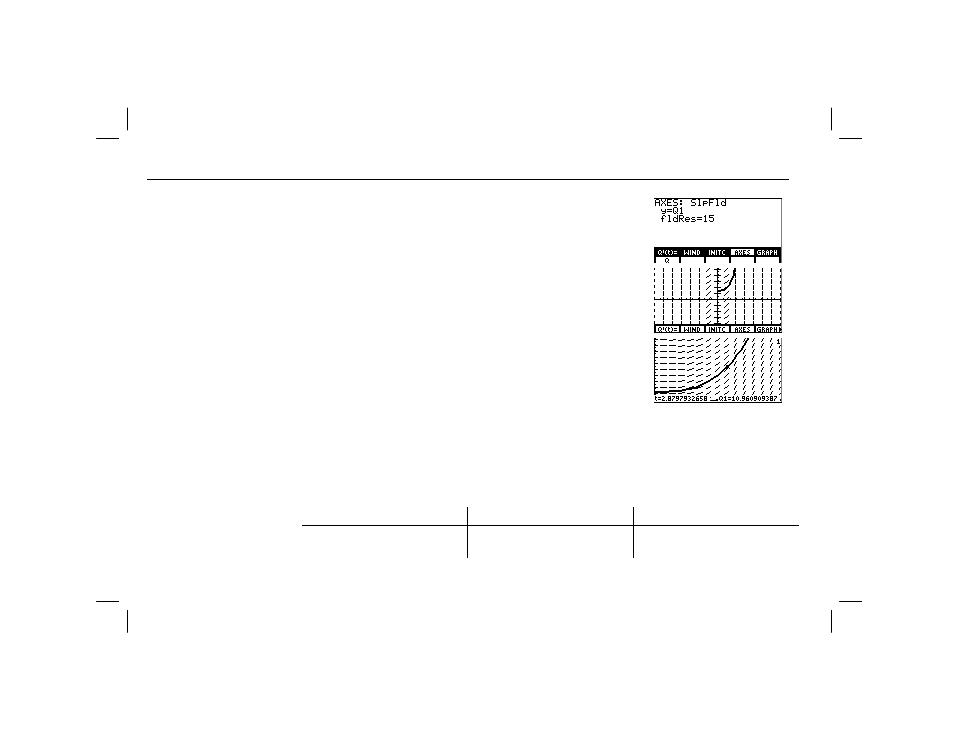
ᕥ Display the axes editor and enter the
equation variable for which you want to
solve. (Do not set
y=Q .)
ᕦ Accept or change fldRes (resolution).
) & 1
ᕧ Display the graph. With the default
window variable values set, the slope
fields for this graph are not very
illustrative.
- i
ᕨ Change the window variables xMin , xMax ,
yMin , and yMax .
ᕩ Select TRACE from the GRAPH menu to re-
plot the graph and activate the trace cursor.
Trace the solution. The trace cursor
coordinates for
t and Q1 are displayed.
' # # # # 0
# 5 # # 0 # 20
/ )
" and !
Transforming an Equation into a First-Order System
On the TI -86, to enter a second-order or higher (up to ninth-order) differential equation, you
must transform it to a system of first-order differential equations. For example, to enter the
second-order differential equation y''=
L y, you must transform it to two first-order
differential equations, as shown in the chart below.
Differentiate... Define the variables as... And then substitute:
Q'1 =y' Q1 =y Q'1=Q2 (since Q'1 =y'= Q2 )
Q'2 =y'' Q2 =y' Q'2= L Q1
In SlpFld field format, x=t is
always true; y=Q1 and
fldRes=15
are the default
axes settings.