Brookfield DV-I Prime - Manual (Page 31)

Brookfield Engineering Laboratories, Inc. Page 31 Manual No. M/07-022-D0613
II.12 Math Models
Math models provide parameters that indicate how materials will behave in various circumstances
where shear stress and shear rate vary. The data and calculated model parameters can be used
to help QC and R&D characterize how a product will behave for the customer and how it will
behave during processing.
When selecting a math model, it is important to take into consideration the parameters that need
to be measured, as well as, the confidence of fit (CoF). A CoF above 98 is recommended. This
appendix discusses the parameters of the following four models, what kinds of materials they
should be used with, and provides an example of each. All models discussed are available with
Brookfield’s Rheocalc™, Wingather™, and RHEO 3000™ software.
• Power Law (Ostwald)
• Herschel-Bulkley
• Bingham
• Casson
In addition to the above models, this section also briefly covers the NCA/CMA Casson model
and the IPC Paste Model. These can be found at the end of this section.
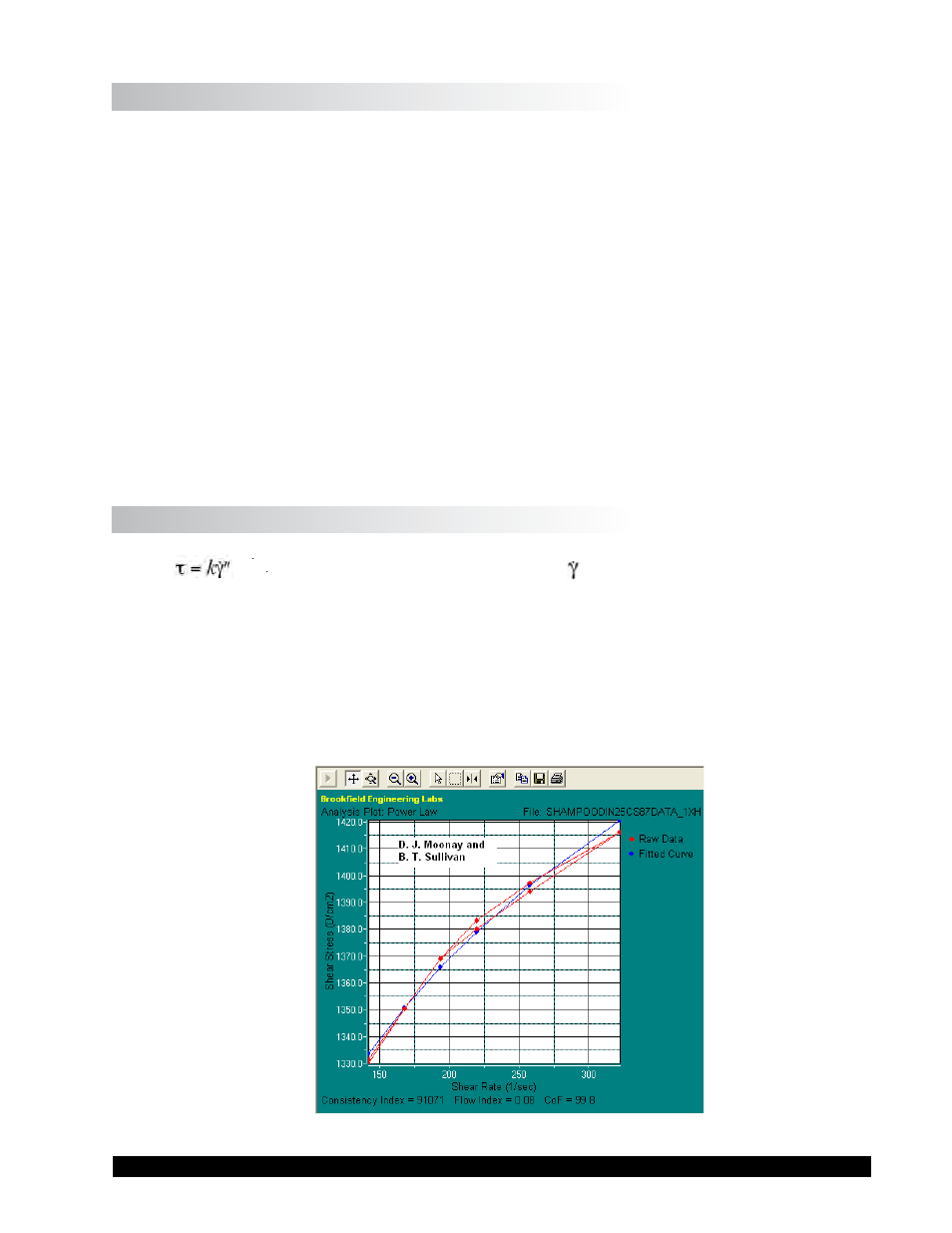
II.12.1 The Power Law (Ostwald) Model
(
€
t = shear stress, k = consistency index, = shear rate, and n = flow index)
What does it tell you?
The Power Law model provides a consistency index, k, which is a product’s viscosity at one
reciprocal second. (Reciprocal seconds are the units of measurement for shear rate.) It also
provides a flow index, n, which indicates the degree with which a material exhibits non-Newtonian
flow behavior. Since Newtonian materials have linear shear stress vs. shear rate behavior and
n
describes the degree of non-Newtonian flow, the flow index essentially indicates how
“non-linear” a material is.
Figure II-43