Digilent 410-274P-KIT - Manual (Page 28)

Nexys4™ FPGA Board Reference Manual
Copyright Digilent, Inc. All rights reserved.
Other product and company names mentioned may be trademarks of their respective owners.
Page 28 of 29
15.1 Pulse-Width Modulation
A pulse-width modulated (PWM) signal is a chain of pulses at some fixed frequency, with each pulse potentially
having a different width. This digital signal can be passed through a simple low-pass filter that integrates the digital
waveform to produce an analog voltage proportional to the average pulse width over some interval (the interval is
determined by the 3dB cut-off frequency of the low pass filter and the pulse frequency). For example, if the pulses
are high for an average of 10% of the available pulse period, then an integrator will produce an analog value that is
10% of the Vdd voltage. Figure 31 shows a waveform represented as a PWM signal.
Vdd
Gnd
Pulse Window
Pulse Width Digital Signal Analog Signal (PWMA)
= 1 / Pulse Frequency (f)
The PWM signal must be integrated to define an analog voltage. The low pass filter 3dB frequency should be an
order of magnitude lower than the PWM frequency, so that signal energy at the PWM frequency is filtered from
the signal. For example, if an audio signal must contain up to 5KHz of frequency information, then the PWM
frequency should be at least 50KHz (and preferably even higher). In general, in terms of analog signal fidelity, the
higher the PWM frequency, the better. Figure 32 shows a representation of a PWM integrator producing an output
voltage by integrating the pulse train. Note the steady-state filter output signal amplitude ratio to Vdd is the same
as the pulse width duty cycle (duty cycle is defined as pulse-high time divided by pulse-window time).
-100
-80
-60
-40
-20
0
20
1 10 100 1K 10K 100K 1M
M
A
G
N
ITUD
E (
D
B)
FREQUENCY (HZ)
Stage II Stage I Overall
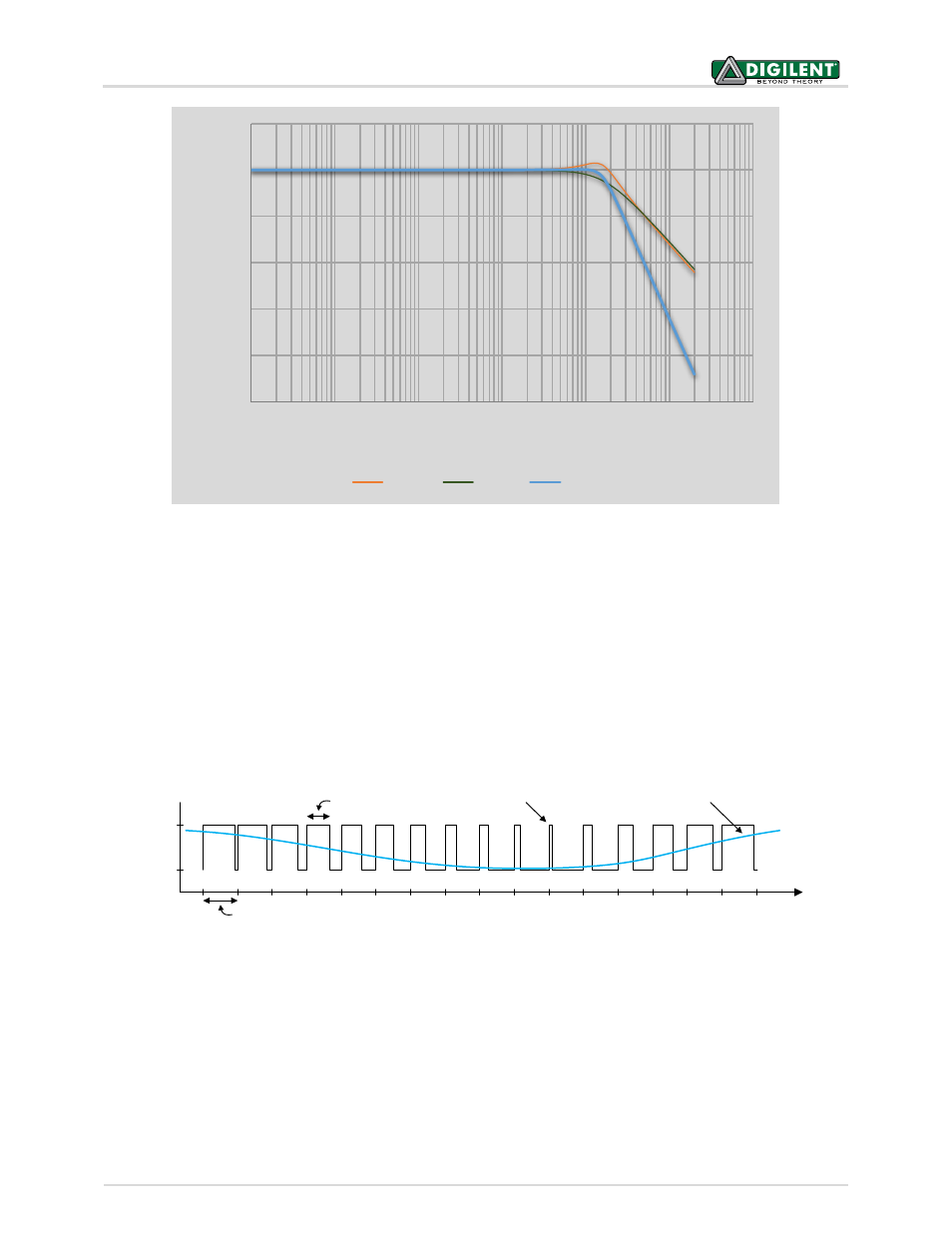
Figure 30. SK Butterworth Low Pass Filter frequency response
Figure 31. Simple Waveform represented as PWM