Casio FX-9750GII - Manual (Page 157)

6-17
• Linear Regression ( ax + b ).............
( a + bx ).............
• Quadratic Regression.....................
• Cubic Regression ...........................
• Quartic Regression ........................
• Logarithmic Regression..................
• Exponential Repression ( a · e bx ) .......
( a · b x )........
• Power Regression ..........................
• Sin Regression ...............................
• Logistic Regression ........................
S Estimated Value Calculation for Regression Graphs
The STAT mode also includes a Y-CAL function that uses regression to calculate the estimated
y -value for a particular x -value after graphing a paired-variable statistical
regression.
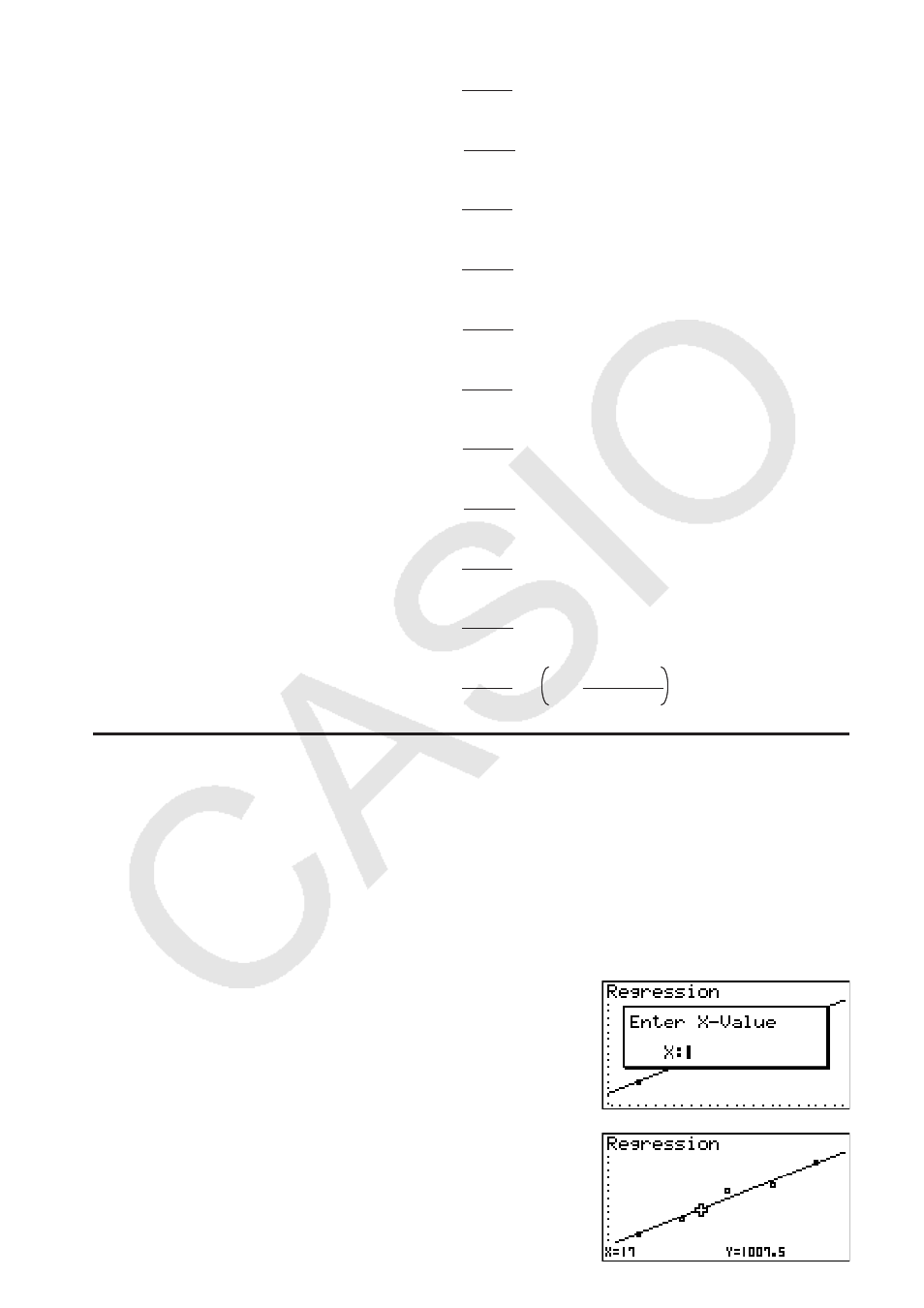
The following is the general procedure for using the Y-CAL function.
1. After drawing a regression graph, press
selection mode, and then press U.
If there are multiple graphs on the display, use D and A to select the graph you want,
and then press U.
• This causes an x -value input dialog box to appear.
2. Input the value you want for x and then press U.
• This causes the coordinates for x and y to appear at
the bottom of the display, and moves the pointer to the
corresponding point on the graph.
MSe =
1
n – 2
i =1
n
(y
i
– (ax
i
+ b)) 2 MSe =
1
n – 2
i =1
n
(y
i
– (ax
i
+ b)) 2
MSe =
1
n – 2
i =1
n
(y
i
– (a + bx
i
)) 2 MSe =
1
n – 2
i =1
n
(y
i
– (a + bx
i
)) 2
MSe =
1
n – 3
i =1
n
(y
i
– (ax
i
+ bx
i
+ c)) 2 2 MSe =
1
n – 3
i =1
n
(y
i
– (ax
i
+ bx
i
+ c)) 2 2
MSe =
1
n – 4
i =1
n
(y
i
– (ax
i
3 + bx
i
+ cx
i
+ d )) 2 2 MSe =
1
n – 4
i =1
n
(y
i
– (ax
i
3 + bx
i
+ cx
i
+ d )) 2 2
MSe =
1
n – 5
i =1
n
(y
i
– (ax
i
4 + bx
i
3 + cx
i
+ dx
i
+ e)) 2 2 MSe =
1
n – 5
i =1
n
(y
i
– (ax
i
4 + bx
i
3 + cx
i
+ dx
i
+ e)) 2 2
MSe =
1
n – 2
i =1
n
(y
i
– (a + b ln x
i
)) 2 MSe =
1
n – 2
i =1
n
(y
i
– (a + b ln x
i
)) 2
MSe =
1
n – 2
i =1
n
(ln y
i
– (ln a + bx
i
)) 2 MSe =
1
n – 2
i =1
n
(ln y
i
– (ln a + bx
i
)) 2
MSe =
1
n – 2
i =1
n
(ln y
i
– (ln a + (ln b) · x
i
)) 2 MSe =
1
n – 2
i =1
n
(ln y
i
– (ln a + (ln b) · x
i
)) 2
MSe =
1
n – 2
i =1
n
(ln y
i
– (ln a + b ln x
i
)) 2 MSe =
1
n – 2
i =1
n
(ln y
i
– (ln a + b ln x
i
)) 2
MSe =
1
n – 2
i =1
n
(y
i
– (a sin (bx
i
+ c) + d )) 2 MSe =
1
n – 2
i =1
n
(y
i
– (a sin (bx
i
+ c) + d )) 2
MSe =
1
n – 2 1 + ae –bx i
C
i =1
n
y
i
–
2
MSe =
1
n – 2 1 + ae –bx i
C
i =1
n
y
i
–
2