Casio FX-9750GII - Manual (Page 150)

6-10
Example Input the two sets of data shown below and plot the data on a scatter
diagram. Next, perform logarithmic regression on the data to display the
regression parameters, and then draw the corresponding regression
graph.
0.5, 1.2, 2.4, 4.0, 5.2 ( x List)
–2.1, 0.3, 1.5, 2.0, 2.4 ( y List)
K STAT
?
DU@
AUA
CUCUD
AUC
A
@U?
BU@
DUAUA
CU
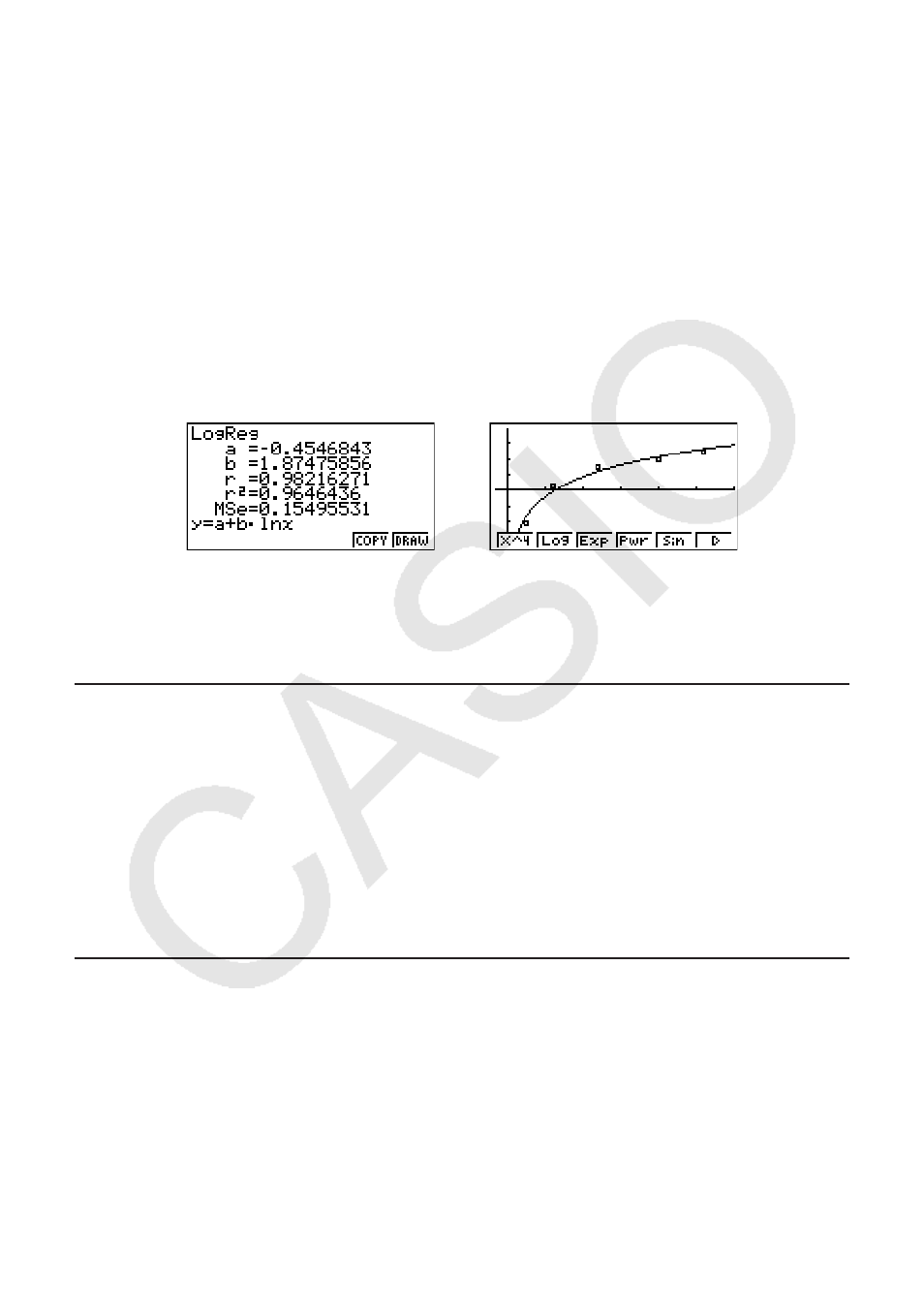
(GRPH)(SET)A(Scat))(GPH1)
(CALC)(E)(Log)
(DRAW)
• You can perform trace on a regression graph. You cannot perform trace scroll.
• Input a positive integer for frequency data. Other types of values (decimals, etc.) cause an
error.
I Selecting the Regression Type
After you graph paired-variable statistical data, you can use the function menu at the bottom of
the display to select from a variety of different types of regression.
• { ax + b }/{ a + bx }/{Med}/{X^2}/{X^3}/{X^4}/{Log}/{ ae ^ bx }/{ ab ^ x }/{Pwr}/{Sin}/{Lgst} ...
{linear regression ( ax + b form)}/{linear regression ( a + bx form)}/{Med-Med}/{quadratic
regression}/{cubic regression}/{quartic regression}/{logarithmic regression}/{exponential
regression (
ae bx form)}/{exponential regression ( ab x form)}/{power regression}/
{sinusoidal regression}/{logistic regression} calculation and graphing
• {2VAR}... {paired-variable statistical results}
I Displaying Regression Calculation Results
Whenever you perform a regression calculation, the regression formula parameter (such as a
and b in the linear regression y = ax + b ) calculation results appear on the display. You can use
these to obtain statistical calculation results.
Regression parameters are calculated as soon as you press a function key to select a
regression type, while a graph is on the display.
The following parameters are used by linear regression, logarithmic regression, exponential
regression, and power regression.
r .............. correlation coefficient
r 2 ............. coefficient of determination
MSe ......... mean square error