PASCO ME-8950A COMPLETE ROTATIONAL SYSTEM User Manual
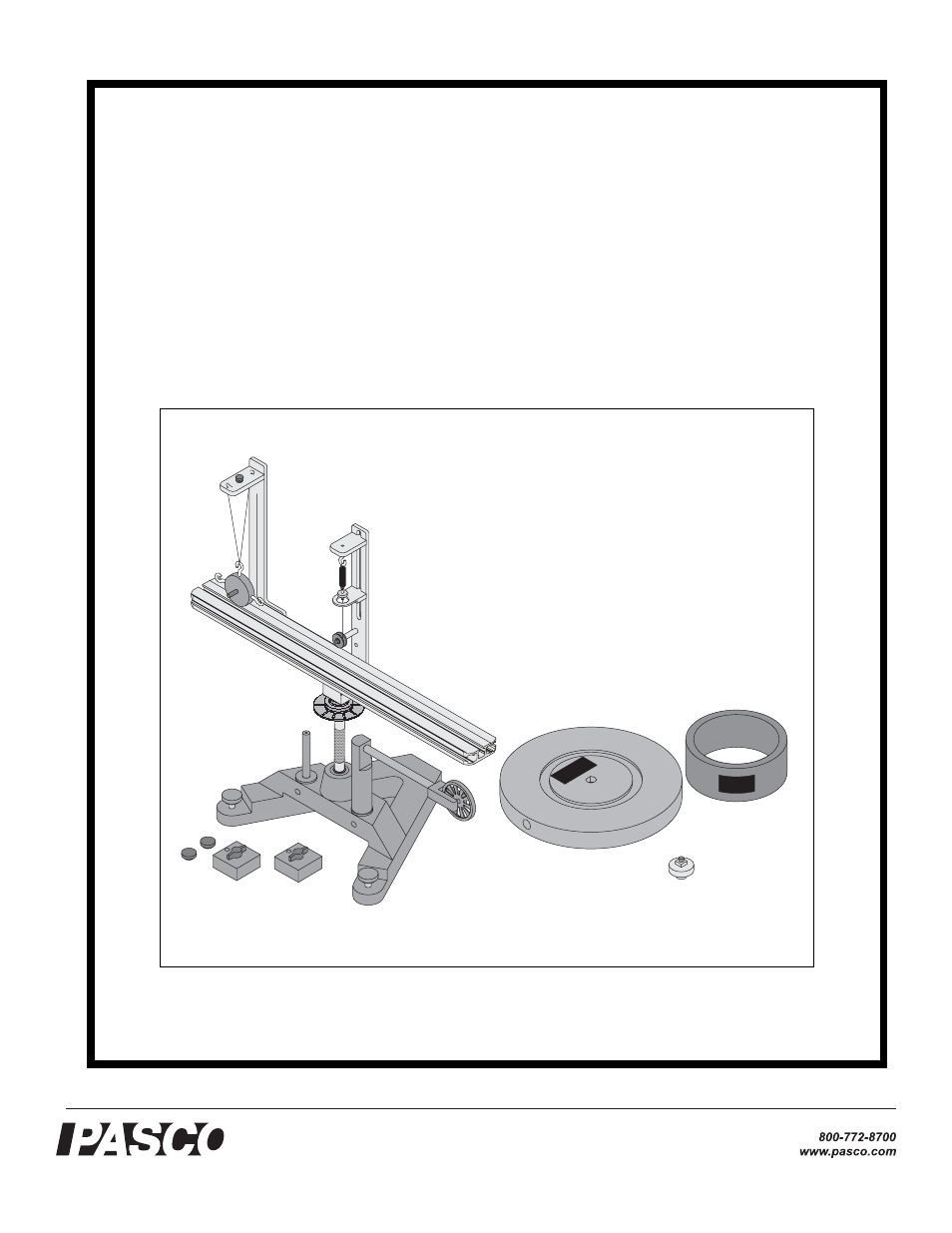
Complete rotational system
Table of contents
Document Outline
- Instruction Manual and Experiment Guide for the PASCO scientific Model ME-8950A
- COMPLETE ROTATIONAL SYSTEM
- introduction.pdf
- assembly.pdf
- "A" base
- Assembly
- 1. Insert the cylindrical end of the shaft into the bearings on the top-side of the A-shaped iron base. Secure the shaft in place by inserting the "E" ring in the slot at the bottom of the shaft. See Figure 1.
- 2. Mount the track to the shaft and tighten the thumb screw against the flat side of the “D” on the shaft. See Figure 1.
- 1. Purposely make the apparatus unbalanced by attaching the 300 g square mass onto either end of the aluminum track. Tighten the...
- 2. Adjust the leveling screw on one of the legs of the base until the end of the track with the square mass is aligned over the leveling screw on the other leg of the base. See Figure 2.
- 3. Rotate the track 90 degrees so it is parallel to one side of the “A” and adjust the other leveling screw until the track will stay in this position.
- 4. The track is now level and it should remain at rest regardless of its orientation.
- 1. Mount the Photogate Head on the threaded end of the photogate mount rod.
- 2. Remove the swivel clamp from the top of the Photogate Head.
- 3. Slide the non-threaded end of the photogate mount rod into a hole in the A-base and clamp it in place with the thumbscrew.
- 4. Adjust the Photogate Head so that its infrared beam can be interrupted by the 10 spoke pulley on the vertical shaft as the shaft turns.
- 5. Connect the cable to the Photogate Head and a PASCO interface.
- 6. When the Photogate Head is powered by a computer interface, you can tell when the photogate is blocked by watching the LED indicator on the photogate.
- 1. Attach the Super Pulley -- and the Photogate Head if needed -- to the Pulley Mounting Rod.
- 2. Insert the pulley mounting rod into the hole in the Accessory Mounting Rod and tighten the thumb screw. See Figure 4.
- 3. Rotate the accessory mounting rod so that a string from the pulley on the center shaft will be aligned with the groove on the Super Pulley.
- 4. Adjust the position of the base so the string passing over the Super Pulley will clear the edge of the table.
- 1. Attach one end of the spring to the spring bracket and connect the indicator disk to the other end of the spring. Insert the spring bracket into the slot on the center post and tighten the thumb screw.
- 2. Tie one end of a string (about 30 cm long) to the bottom of the indicator disk and tie a loop in the other end of the string.
- 3. Insert the indicator bracket into the slot on the center post, placing it below the spring bracket. Tighten the thumb screw.
- 4. Attach the pulley in the higher of the two holes on the center bracket.
- 5. Insert the thumb screw at the bottom of the center post and attach the square nut.
- 1. Insert the thumb screw at the bottom of the side post and attach the square nut.
- 2. Using a string about 30 cm long, tie the string around the screw head on the top of the side post. Then thread the other end ...
- 3. Loosen the screw on the top of the side post and wrap the loose end of the string around the threads of the screw and tighten the screw.
- 1. Mount the center post in the T-slot on the side of the track that has the rule. Align the line on the center post with the ze...
- 2. Hang the 100 g mass from the string on the side post and adjust the height of the mass so the string coming from the center post will be level when the mass is hanging straight down.
- 1. Attach the square nut (supplied with the Rotational Inertia Accessory) to the platform adapter.
- 2. Position the platform adapter at the desired radius as shown in Figure 8.
- 3. Grip the knurled edge of the platform adapter and tighten.
- "A" base
- rotating platform
- "E" ring
- vertical shaft
- thumbscrew
- flat of vertical shaft
- Figure 1: Attaching the Vertical Shaft to the Base and Rotating Platform Assembly
- Figure 2: Leveling the Base
- Figure 3: Using the Photogate Mount Rod With the Photogate Head
- Figure 4: Using the Accessory Mounting Rod With the Pulley Mounting Rod, Super Pulley, and Photogate Head
- Figure 5: Center Post Assembly
- Figure 6: Side Post Assembly
- Figure 7: Threading the Centripetal Force Accessory
- Figure 8: Rotational Inertia Accessory Including Platform Adapter Assembly
- X1-3.pdf
- Projectile Catcher
- step pulley
- Part I: Determining the initial velocity of the ball
- 1. Clamp the Projectile Launcher to a sturdy table near one end of the table.
- 2. Adjust the angle of the Projectile Launcher to zero degrees so the ball will be shot off horizontally. See Figure 1.3.
- 1. Put the ball into the Projectile Launcher and cock it to the long range position. Fire one shot to locate where the ball hits...
- 2. Fire about ten shots.
- 3. Measure the vertical distance from the bottom of the ball as it leaves the barrel (this position is marked on the side of the barrel) to the floor. Record this distance in Table 1.1.
- 4. Use a plumb bob to find the point on the floor that is directly beneath the release point on the barrel. Measure the horizontal distance along the floor from the release point to the leading edge of the paper. Record in Table 1.1.
- 5. Measure from the leading edge of the paper to each of the ten dots and record these distances in Table 1.1.
- 6. Find the average of the ten distances and record in Table 1.1.
- 7. Using the vertical distance and the average horizontal distance, calculate the time of flight and the initial velocity of the ball. Record in Table 1.1 and Table 1.4.
- 1. Attach the photogate bracket to the Launcher and attach two Photogates to the bracket. Plug the Photogates into a computer or other timer.
- 2. Put the ball into the Projectile Launcher and cock it to the long range position.
- 3. Run the DataStudio program. Set it to measure the time between the ball blocking the two Photogates as it comes out of the Launcher.
- 4. Shoot the ball three times and take the average of these times. Record in Table 1.2.
- 5. The distance between the Photogates is 10 cm. Calculate the initial speed and record it in Table 1.2 and Table 1.4.
- Part II: Conservation of Angular Momentum
- 1. Find the mass of the ball and record it in Table 1.3.
- 2. Attach the ball catcher to the track using a rubber band as shown in Figure 1.4.
- 3. With the Projectile Launcher mounted as it was in Part I, aim the launcher directly down the middle of the ball catcher using the sights inside the projectile launcher. Clamp the launcher to the table.
- 4. Attach the Photogate Head to the base. Connect the Photogate Head to a computer and run the DataStudio program.
- 5. Set up the program so that it measures and displays angular speed.
- 1. Level the rotating platform.
- 2. Load the Launcher with the steel ball on the long range setting.
- 3. Make sure the rotating platform is at rest and fire the ball into the catcher. Record the angular speed of the platform in Table 1.3. Repeat for a total of five shots.
- 4. Measure the distance from the axis of rotation to the ball in the catcher and record in Table 1.3.
- Part III: Determining the Rotational Inertia
- 1. Attach a Photogate with a pulley and mounting rod to the base using the black rod.
- 2. Connect the Photogate to a PASCO interface and connect the interface to a computer.
- 3. Wind a thread around the middle step pulley on the center shaft and pass the thread over the pulley.
- 1. Start the DataStudio program. Select ’Smart Pulley (Linear)’ and set up a Digits display to show velocity with three significant figures.
- 2. Hang a small amount of mass such as a few paper clips on the end of the thread that is over the pulley.
- 3. Start monitoring data, and then give the Rotating Platform a tap to get it started moving.
- 4. Watch the Digits display to see the velocity.
- 5. If the velocity increases or decreases as the Rotating Platform turns, stop monitoring data, stop the Rotating Platform, and adjust the amount of mass on the thread by adding or removing a paper clip.
- 6. Repeat the process until the velocity stays constant.
- 7. Measure the mass on the end of the thread and record it as the ’Friction Mass’ in Table 1.4.
- 1. Wind the thread up and hold the Rotating Platform.
- 2. Let the Rotating Platform begin to turn and at the same time, start recording data.
- 3. Let the mass descend toward the floor but STOP recording data just before the mass hits the floor.
- 4. Examine your Graph display of Velocity versus Time. The slope of the best fit line for your data is the acceleration of the apparatus.
- 5. Record the slope in Table 1.4.
- 1. Using calipers, measure the diameter of the step pulley about which the thread is wrapped and calculate the radius.
- 2. Record the radius in Table 1.4.
- 1. Calculate the average of the angular speeds in Table 1.3 and record the result in Table 1.5.
- 2. Calculate the rotational inertia:
- 3. Using the average angular speed, the rotational inertia, and the distance, r, calculate the muzzle velocity of the ball and record it in Table 1.5.
- 4. Calculate the percent difference between the muzzle velocities found in Parts I and II. Record in Table 1.5.
- 1. What percentage of the kinetic energy is lost in the collision? Use the masses and velocities to calculate this percentage.
- Experiment 3: Centripetal Force
- Part I: Vary Radius (constant force and mass)
- 1. The centripetal force and the mass of the hanging object will be held constant for this part of the experiment. Weigh the obj...
- 2. Attach the clamp-on pulley to the end of the track nearer to the hanging object. Attach a string to the hanging object and hang a known mass over the clamp-on pulley. Record this mass in Table 3.1. This establishes the constant centripetal force.
- 3. Select a radius by aligning the line on the side post with any desired position on the measuring tape. While pressing down on...
- 4. The object on the side bracket must hang vertically: On the center post, adjust the spring bracket vertically until the string from which the object hangs on the side post is aligned with the vertical line on the side post.
- 5. Align the indicator bracket on the center post with the orange indicator.
- 6. Remove the mass that is hanging over the pulley and remove the pulley.
- 7. Rotate the apparatus by hand, increasing the speed until the orange indicator is centered in the indicator bracket on the cen...
- 8. Maintaining this speed, use a stopwatch to time ten revolutions. Divide the time by ten and record the period in Table 3.1.
- 9. Move the side post to a new radius and repeat the procedure. Do this for a total of five radii.
- 1. The weight of the mass hanging over the pulley is equal to the centripetal force applied by the spring. Calculate this force by multiplying the mass hung over the pulley by “g” and record this force at the top of Table 3.2.
- 2. Calculate the square of the period for each trial and record this in Table 3.1.
- 3. Plot the radius versus the square of the period. This will give a straight line since:
- 4. Draw the best-fit line through the data points and measure the slope of the line. Record the slope in Table 3.1.
- 5. Calculate the centripetal force from the slope and record in Table 3.2.
- 6. Calculate the percent difference between the two values found for the centripetal force and record in Table 3.2.
- Part II: Vary Force (constant radius and mass)
- 1. Weigh the object and record its mass in Table 3.3. Hang the object from the side post and connect the string from the spring to the object. The string must pass under the pulley on the center post.
- 2. Attach the clamp-on pulley to the end of the track nearer to the hanging object. Attach a string to the hanging object and hang a known mass over the clamp-on pulley. Record this mass in Table 3.3. This determines the centripetal force.
- 3. Select a radius by aligning the line on the side post with any desired position on the measuring tape. While pressing down on...
- 4. The object on the side bracket must hang vertically: On the center post, adjust the spring bracket vertically until the string from which the object hangs on the side post is aligned with the vertical line on the side post.
- 5. Align the indicator bracket on the center post with the orange indicator.
- 6. Remove the mass that is hanging over the pulley and remove the pulley.
- 7. Rotate the apparatus, increasing the speed until the orange indicator is centered in the indicator bracket on the center post...
- 8. Maintaining this speed, use a stopwatch to time ten revolutions. Divide the time by ten and record the period in Table 3.3.
- 9. To vary the centripetal force, clamp the pulley to the track again and hang a different mass over the pulley. Keep the radius constant and repeat the procedure from Step #4. Do this for a total of five different forces.
- 1. The weight of the mass hanging over the pulley is equal to the centripetal force applied by the spring. Calculate this force for each trial by multiplying the mass hung over the pulley by “g” and record the results in Table 3.3.
- 2. Calculate the inverse of the square of the period for each trial and record this in Table 3.3.
- 3. Plot the centripetal force versus the inverse square of the period. This will give a straight line since:
- 4. Draw the best-fit line through the data points and measure the slope of the line. Record the slope in Table 3.3.
- 5. Calculate the mass of the object from the slope and record in Table 3.4.
- 6. Calculate the percent difference between the two values found for the mass of the object and record in Table 3.4.
- Part III: Vary Mass (constant radius and force)
- 1. Weigh the object with the additional side masses in place. Record its mass in Table 3.5. Hang the object from the side post and connect the string from the spring to the object. The string must pass under the pulley on the center post.
- 2. Attach the clamp-on pulley to the end of the track nearer to the hanging object. Attach a string to the hanging object and hang a known mass over the clamp-on pulley. Record this mass in Table 3.5. This establishes the constant centripetal force.
- 3. Select a radius by aligning the line on the side post with any desired position on the measuring tape. While pressing down on...
- 4. The object on the side bracket must hang vertically: On the center post, adjust the spring bracket vertically until the string from which the object hangs on the side post is aligned with the vertical line on the side post.
- 5. Align the indicator bracket on the center post with the orange indicator.
- 6. Remove the mass that is hanging over the pulley and remove the pulley.
- 7. Rotate the apparatus, increasing the speed until the orange indicator is centered in the indicator bracket on the center post...
- 8. Maintaining this speed, use a stopwatch to time ten revolutions. Divide the time by ten and record the period in Table 3.5.
- 9. Vary the mass of the object by removing the side masses. Keep the radius constant and measure the new period. Weigh the object again and record the mass and period in Table 3.5.
- 1. The weight of the mass hanging over the pulley is equal to the centripetal force applied by the spring. Calculate this force by multiplying the mass hung over the pulley by “g” and record the result at the top of Table 3.5.
- 2. Calculate the centripetal force for each trial using:
- 3. Calculate the percent difference between the calculated centripetal force for each trial and mg. Record in Table 3.5.
- 1. When the radius is increased, does the period of rotation increase or decrease?
- 2. When the radius and the mass of the rotating object are held constant, does increasing the period increase or decrease the centripetal force?
- 3. As the mass of the object is increased, does the centripetal force increase or decrease?
- Projectile Launcher
- Rotating Platform
- "A" base
- Projectile Collision Accessory ("catcher")
- vo
- w
- Photogate with pulley
- Figure 1.1 Conservation of Angular Momentum
- Figure 1.2: Rotational Apparatus and Free-Body Diagram
- Figure 1.3 Projectile Launcher Setup
- Table 1.1 Determining the Initial Velocity
- Table 1.2 Initial Speed Using Photogates
- Figure 1.4: Attaching the Catcher to the Track
- Table 1.3 Angular Speed
- Table 1.4 Rotational Inertia Data
- Table 1.5 Results
- Experiment 2: Rotational Inertia of a Point Mass
- 1. Level the rotating platform.
- 2. Attach the square mass (point mass) to the track on the rotating platform at any radius you wish.
- 3. Mount the Photogate/Pulley system to the base and connect the photogate through an interface to a computer. See Figure 2.2.
- 4. Attach a thread to the middle step of the step pulley and hang the thread over the 10-spoke pulley. Allow the string to reach to the floor.
- Experiment 2: Rotational Inertia of a Point Mass
- Part I: Measurements For the Theoretical Rotational Inertia
- Part II: Measurement For the Experimental Method
- 1. Start the DataStudio program. Select ’Smart Pulley (Linear)’ and set up a Digits display to show velocity with three significant figures.
- 2. Hang a small amount of mass - such as a few paper clips - on the end of the thread that is over the pulley.
- 3. Start monitoring data, and then give the Rotating Platform a tap to get it started moving.
- 4. Watch the Digits display to see the velocity.
- mg
- T
- a
- rotating platform
- "A" base
- hanging mass
- Figure 2.1: Rotational Apparatus and Free-Body Diagram
- Table 2.1: Theoretical Rotational Inertia
- Figure 2.2: Rotational inertia of a point mass
- rotating platform
- "A" base
- 10-spoke pulley with photogate head
- 300g mass
- 5. If the velocity increases or decreases as the platform turns, stop monitoring data, stop the platform, and adjust the amount of mass on the thread by adding or removing a paper clip.
- 6. Repeat the process until the velocity stays constant as the mass falls.
- 7. Measure the mass on the end of the thread and record it as the ’Friction Mass’ in Table 2.2.
- 1. Wind the thread up and hold the Rotating Platform.
- 2. Let the platform begin to turn and at the same time, start recording data.
- 3. Let the mass fall toward the floor but STOP recording data just before the mass hits the floor.
- 4. Examine your Graph display of Velocity versus Time. The slope of the best ’Linear Fit’ for your data is the acceleration of the apparatus.
- 5. Record the slope in Table 2.2.
- 1. Using calipers, measure the diameter of the step pulley about which the thread is wrapped and calculate the radius.
- 2. Record the radius in Table 2.2.
- 1. Take the point mass off the rotational apparatus and repeat Finding the Acceleration of the Point Mass and Apparatus for the apparatus alone.
- 2. Record the data in Table 2.2.
- 1. Subtract the “friction mass” from the hanging mass used to accelerate the apparatus to determine the mass, m, to be used in the equations.
- 2. Calculate the experimental value of the rotational inertia of the point mass and apparatus together and record in Table 2.3.
- 3. Calculate the experimental value of the rotational inertia of the apparatus alone. Record in Table 2.3.
- 4. Subtract the rotational inertia of the apparatus from the combined rotational inertia of the point mass and apparatus. This will be the rotational inertia of the point mass alone. Record in Table 2.3.
- 5. Calculate the theoretical value of the rotational inertia of the point mass. Record in Table 2.3.
- 6. Use a percent difference to compare the experimental value to the theoretical value. Record in Table 2.3.
- Table 2.2: Rotational Inertia Data
- Table 2.3: Results
- Figure 3.1: Centripetal Force Apparatus
- Table 3.1: Varying the Radius
- Table 3.2: Results (varying raduis)
- Table 3.3: Varying the Centripetal Force
- Table 3.4: Results (varying the centripetal force)
- Table 3.5: Varying the Mass of the Object
- Notes:
- X4-7.pdf
- Experiment 4: Conservation of Angular Momentum Using a Point Mass
- Part I: Conservation of Angular Momentum
- 1. Level the apparatus using the square on the track as shown in the leveling instructions in the Assembly Section.
- 2. Slide a thumb screw and square nut into the T-slot on the top of the track and tighten it down at about the 5 cm mark. This will act as a stop for the sliding square mass. See Figure 4.2.
- 3. With the side of the square mass that has the hole oriented toward the center post, slide the square mass onto the track by i...
- 4. Slide a second thumb screw and square nut into the T-slot and tighten it down at about the 20 cm mark. Now the square mass is free to slide between the two limiting stops.
- 5. Move the pulley on the center post to its lower position. Remove the spring bracket from the center post and set it aside.
- 6. Attach a string to the hole in the square mass and thread it around the pulley on the center post and pass it through the indicator bracket.
- 7. Mount the Photogate on the rod on the base and position it so it straddles the holes in the pulley on the center rotating shaft.
- 8. Start the DataStudio program. Connect the Photogate to a PASCO interface and connect the interface to a computer (if needed).
- 1. Select ’Smart Pulley (Rotational)’ as the type of sensor. Set up a Graph display of Velocity (rad/s) versus time.
- 2. Hold the string just above the center post. With the square mass against the outer stop, give the track a spin using your hand.
- 3. Click ’Start’ to begin recording data. After about 20 data points have been taken, pull up on the string to cause the square mass to slide from the outer stop to the inner stop.
- 4. Continue to hold the string up and take about 20 data points after pulling up on the string. Click ’Stop’ to end recording data.
- 5. Examine the Graph display of Velocity (rad/s) versus time. The graph shows the angular speed before and after the square mass is pulled toward the inner stop. Rescale the graph if necessary.
- 6. Use the Smart Cursor tool to determine the angular speed immediately before and immediately after pulling the string. Record these values in Table 4.1.
- 7. Repeat the experiment a total of three times with different initial angular speeds. Record these values in Table 4.1.
- Part II: Determining the Rotational Inertia
- 1. Attach a Photogate with Pulley to a mounting rod and attach the mounting rod to the black support rod on the base.
- 2. Wind a thread around the pulley on the center shaft and pass the thread over the Pulley. See Figure 4.3.
- 1. Start the DataStudio program. Select ’Smart Pulley (Linear)’ and set up a Digits display to how velocity with three significant figures.
- 2. Hang a small amount of mass (such as a few paper clips) on the end of the thread that is over the pulley. Make sure that the thread is wound around the step pulley.
- 3. Start monitoring data, and then give the Rotating Platform a tap to get it started moving.
- 4. Watch the Digits display to see the velocity.
- 5. If the velocity increases or decreases as the platform turns, stop monitoring data, stop the platform, and adjust the amount of mass on the end of the thread.
- 6. Repeat the process until the velocity stays constant.
- 7. Measure the mass on the end of the thread and record it as ’Friction Mass’ in Table 4.2..
- 1. Wind the thread up and hold the Rotating Platform.
- 2. Let the Rotating Platform begin to turn and at the same time, START recording data.
- 3. Let the mass descend toward the floor but STOP recording data just before the mass hits the floor.
- 4. Examine your graph of velocity versus time. The slope ("m") of the best fit line for your data is the acceleration (use Fit>Linear Fit). Record the slope in Table 4.2.
- 1. Using calipers, measure the diameter of the step pulley about which the thread is wrapped and calculate the radius.
- 2. Record the radius in Table 4.2.
- mg
- T
- rotating platform
- "A" base
- hanging mass
- a
- Figure 4.1: Rotational Apparatus and Free-Body Diagram
- Figure 4.2: Set-up for conservation of angular momentum
- Table 4.1: Data
- Figure 4.3: Set-up for determining rotational inertia
- 300g mass
- stop screws (2)
- center post
- string
- "A" base
- rotating platform
- hanging mass
- 10-spoke pulley with photogate head
- "A"-base
- 1. Calculate the rotational inertias:
- 2. Calculate the expected (theoretical) values for the final angular velocity and record these values in Table 4.3.
- 3. For each trial, calculate the percent difference between the experimental and the theoretical values of the final angular velocity and record these in Table 4.3.
- 1. Which kinetic energy is greater?
- 2. Why?
- Table 4.2 Rotational Inertia Data
- Table 4.3: Results
- Experiment 5: Rotational Inertia of Disk and Ring
- 1. Remove the track from the Rotating Platform and place the disk directly on the center shaft as shown in Figure 5.4. The side of the disk that has the indentation for the ring should be up.
- 2. Place the ring on the disk, seating it in this indentation.
- 3. Mount the Photogate/Pulley System to the base and connect it to a PASCO interface.
- 4. Attach a thread to the top step of the three-step pulley on the Rotational Apparatus shaft and suspend the string over the pulley of the Photogate/Pulley System. Attach a hanger and mass to the end of the thread.
- 5. Start the DataStudio program.
- 1. Weigh the ring and disk to find their masses and record these masses in Table 5.1.
- 2. Measure the inside and outside diameters of the ring and calculate the radii R1 and R2. Record in Table 5.1.
- 3. Measure the diameter of the disk and calculate the radius R and record it in Table 5.1.
- 1. In the DataStudio program, select ’Smart Pulley (Linear)’ and set up a Digits display to show velocity with three significant figures.
- 2. Hang a small amount of mass such as a few paper clips on the end of the thread that is over the pulley.
- 3. Start monitoring data, and then give the Rotational Disk a tap to get it started moving.
- 4. Watch the Digits display to see the velocity.
- 5. If the velocity increases or decreases as the Rotational Disk turns, stop monitoring data, stop the Rotational Disk, and adjust the amount of mass on the thread by adding or removing a paper clip.
- 6. Repeat the process until the velocity stays constant.
- 7. Measure the mass on the end of the thread and record it as the ’Friction Mass’ in Table 5.2.
- 1. Wind the thread up and hold the Rotating Platform.
- 2. Let the Rotating Platform begin to turn and at the same time, start recording data.
- 3. Let the mass descend toward the floor but STOP recording data just before the mass hits the floor.
- 4. Examine your Graph display of Velocity versus Time. The slope of the best fit line for your data is the acceleration of the apparatus.
- 5. Record the slope in Table 5.2.
- 1. Using calipers, measure the diameter of the cylinder about which the thread is wrapped and calculate the radius. Record in Table 5.2.
- 1. To do this, take the ring off the rotational apparatus and repeat Finding the Acceleration of Ring and Disk for the disk alone.
- 1. Subtract the “friction mass” from the hanging mass used to accelerate the apparatus to determine the mass, m, to be used in the equations.
- 2. Calculate the experimental value of the rotational inertia of the ring and disk together.
- 3. Calculate the experimental value of the rotational inertia of the disk alone.
- 4. Subtract the rotational inertia of the disk from the total rotational inertia of the ring and disk.
- 5. Calculate the experimental value of the rotational inertia of the disk about its diameter.
- 6. Calculate the theoretical value of the rotational inertia of the ring.
- 7. Calculate the theoretical value of the rotational inertia of the disk about its center of mass and about its diameter.
- 8. Use a percent difference to compare the experimental values to the theoretical values.
- Experiment 6: Rotational Inertia of Disk Off-Axis (Fixed/Rotating)
- 1. Set up the Rotational Accessory as shown in Figure 6.2. Mount the disk with its bearing side up. Use the platform adapter to fasten the disk to the track at a large radius.
- 2. Mount two square masses on the opposite end of the platform to act as a counterweight. Be sure to tighten the screws.
- 3. Mount the Photogate/Pulley System to the base and connect it to an interface.
- 4. Run the DataStudio program.
- 1. Weigh the disk to find the mass M.
- 2. Measure the diameter and calculate the radius R.
- 3. Measure the distance, d, from the axis of rotation to the center of the disk.
- 1. In the DataStudio program, select ’Smart Pulley (Linear)’ and set up a Digits display to show velocity with three significant figures.
- 2. Hang a small amount of mass such as a few paper clips on the end of the thread that is over the pulley.
- 3. Start monitoring data, and then give the Rotational Disk a tap to get it started moving.
- 4. Watch the Digits display to see the velocity.
- 5. If the velocity increases or decreases as the Rotational Disk turns, stop monitoring data, stop the Rotational Disk, and adjust the amount of mass on the thread by adding or removing a paper clip.
- 6. Repeat the process until the velocity stays constant.
- 7. Measure the mass on the end of the thread and record it as the ’Friction Mass’ in Table 6.2.
- 1. Wind the thread up and hold the Rotating Platform.
- 2. Let the Rotating Platform begin to turn and at the same time, start recording data.
- 3. Let the mass descend toward the floor but STOP recording data just before the mass hits the floor.
- 4. Examine your Graph display of Velocity versus Time. The slope of the best fit line for your data is the acceleration of the apparatus.
- 5. Record the slope in Table 6.2.
- 1. Using calipers, measure the diameter of the cylinder about which the thread is wrapped and calculate the radius. Record in Table 6.2.
- 1. To do this, take the disk off the rotational apparatus and repeat Finding the Acceleration of Disk and Track for the track alone.
- 1. Subtract the “friction mass” from the hanging mass used to accelerate the apparatus to determine the mass, m, to be used in the equations.
- 2. Calculate the experimental value of the rotational inertia of the fixed disk and track combined.
- 3. Calculate the experimental value of the rotational inertia of the track alone.
- 4. Subtract the rotational inertia of the track from the rotational inertia of the fixed disk and track. This will be the rotational inertia of the fixed disk alone.
- 5. Calculate the experimental value of the rotational inertia of the fixed disk and track combined.
- 6. Subtract the rotational inertia of the track from the rotational inertia of the free disk and track. This will be the rotational inertia of the free disk alone.
- 7. Calculate the theoretical value of the rotational inertia of the fixed disk off axis.
- 8. Calculate the theoretical value of a point mass having the mass of the disk.
- 9. Use a percent difference to compare the experimental values to the theoretical values.
- Experiment 7: Conservation of Angular Momentum
- 1. Level the apparatus using the square mass on the track.
- 2. Assemble the Rotational Inertia Accessory as shown in Figure 7.1. The side of the disk with the indentation for the ring should be up.
- 3. Mount the Photogate on the metal rod on the base and position it so it straddles the holes in the pulley on the center rotating shaft.
- 4. Start the DataStudio program. Select ’Smart Pulley (Rotational)’ as the sensor.
- 5. Set up a Graph display of Velocity (rad/s) versus Time (s).
- 1. Hold the ring just above the center of the disk. Give the disk a spin using your hand.
- 2. Start recording data. After about 25 data points have been taken, drop the ring onto the spinning disk. See Figure 7.2.
- 3. Continue to take data after the collision for a few seconds and then stop recording data.
- 4. Examine the Graph display of the rotational speed versus time. Use the Autoscale tool to resize the axes if necessary.
- 5. In the Graph display, use the Smart Tool to determine the angular velocity immediately before and immediately after the collision. Record these values in Table 7.1.
- 6. Weigh the disk and ring and measure the radii. Record these values in Table 7.1.
- 1. Calculate the expected (theoretical) value for the final angular velocity and record this value in Table 7.1.
- 2. Calculate the percent difference between the experimental and the theoretical values of the final angular velocity and record in Table 7.1.
- 1. Does the experimental result for the angular speed agree with the theory?
- 2. What percentage of the rotational kinetic energy is lost during the collision? Calculate this and record the results in Table 7.1.
- Experiment 5: Rotational Inertia of Disk and Ring
- Figure 5.1: Ring
- Disk about center of Mass
- Disk about Diameter
- Figure 5.2:
- Table 5.1: Theoretical Rotational Inertia
- Figure 5.3: Rotational Apparatus and Free-Body Diagram
- Figure 5.4: Set-up for Disk and Ring
- Table 5.2: Rotational Inertia Data
- Figure 7.1: Assembly for Dropping Ring onto Disk
- Figure 5.5: Disk mounted vertically
- Table 5.3: Results
- Figure 6.1: Rotational Apparatus and Free-Body Diagram
- Figure 6.2: Set-up for Disk Off-Axis
- Table 6.1: Theoretical Rotational Inertia
- Table 6.2: Rotational Inertia Data
- Table 6.3: Results
- Figure 7.2: Experiment Setup
- Table 7.1: Data and Results
- Technical Support