PASCO WA-9611_13 SONOMETER - Manual (Page 12)

8
Sonometer 012-03489E
Theory of Waves on a Stretched String
Resonance
The analysis above assumes that the standing wave is
formed by the superposition of an original wave and one
reflected wave. In fact, if the string is fixed at both ends,
each wave will be reflected every time it reaches either
end of the string. In general, the multiply reflected waves
will not all be in phase, and the amplitude of the wave
pattern will be small. However, at certain frequencies of
oscillation, all the reflected waves are in phase, resulting
in a very high amplitude standing wave. These frequen-
cies are called resonant frequencies.
In Experiment 1, the relationship between the length of
the string and the frequencies at which resonance occurs
is investigated. It is shown that the conditions for reso-
nance are more easily understood in terms of the wave-
length of the wave pattern, rather than in terms of the fre-
quency. In general, resonance occurs when the wave-
length (
λ
) satisfies the condition:
λ
= 2L/n; n = 1, 2, 3, 4,…
Another way of stating this same relationship is to say
that the length of the string is equal to an integral number
of half wavelengths. This means that the standing wave is
such that a node of the wave pattern exists naturally at
each fixed end of the string.
Velocity of Wave Propagation
Assuming a perfectly flexible, perfectly elastic string, the
velocity of wave propagation (V) on a stretched string
depends on two variables: the mass per unit length or lin-
ear density of the string (m) and the tension of the string
(T). The relationship is given by the equation:
V =
T
µ
Without going into the derivation of this equation, its ba-
sic form can be appreciated. The equation is analogous to
Newton’s Second law, providing a relationship between a
measure of force, a measure of inertia, and a quantity of
motion. With this analogy in mind, it makes sense that the
velocity should depend on the tension and linear density
of the string. That the form of the two equations is not ex-
actly the same is to be expected. The motion of the string is
considerably different than the motion of a simple rigid
body acted on by a single force. (It could be asked whether
velocity, rather than acceleration, is the right measure of
motion to focus on. Since the waves on the string do not
accelerate, this is at least a reasonable assumption.)
Standing Waves
A simple sine wave traveling along a taut string can be
described by the equation y
1
= y
m
sin 2
π
(x/
λ
- t/n). If the
string is fixed at one end, the wave will be reflected back
when it strikes that end. The reflected wave will then in-
terfere with the original wave. The reflected wave can be
described by the equation y
2
= y
m
sin 2
π
(x/
λ
+ t/n). As-
suming the amplitudes of these waves are small enough
so that the elastic limit of the string is not exceeded, the
resultant waveform will be just the sum of the two waves:
y = y
1
+ y
2
= y
m
sin 2
π
(x/
λ
- t/
λ
) + y
m
sin 2
π
(x/
λ
+ t/
λ
).
Using the trigonometric identity:
sin A + sin B = 2 sin1/2(A + B) cos1/2(B - A),
this equation becomes:
y = 2y
m
sin (2
π
x/
λ
) cos (2
π
t/
λ
).
This equation has some interesting characteristics. At a
fixed time, t
0
, the shape of the string is a sine wave with a
maximum amplitude of 2y
m
cos (2
π
t
0
/
λ
). At a fixed posi-
tion on the string, x
0
, the string is undergoing simple har-
monic motion, with an amplitude of 2y
m
sin (2
π
x
0
/
λ
).
Therefore, at points of the string where x
0
= l/4, 3l/4, 5l/4,
7l/4, etc., the amplitude of the oscillations will be a maxi-
mum. At points of the string where x
0
= l/2, l, 3l/2, 2l,
etc., the amplitude of the oscillations will be zero.
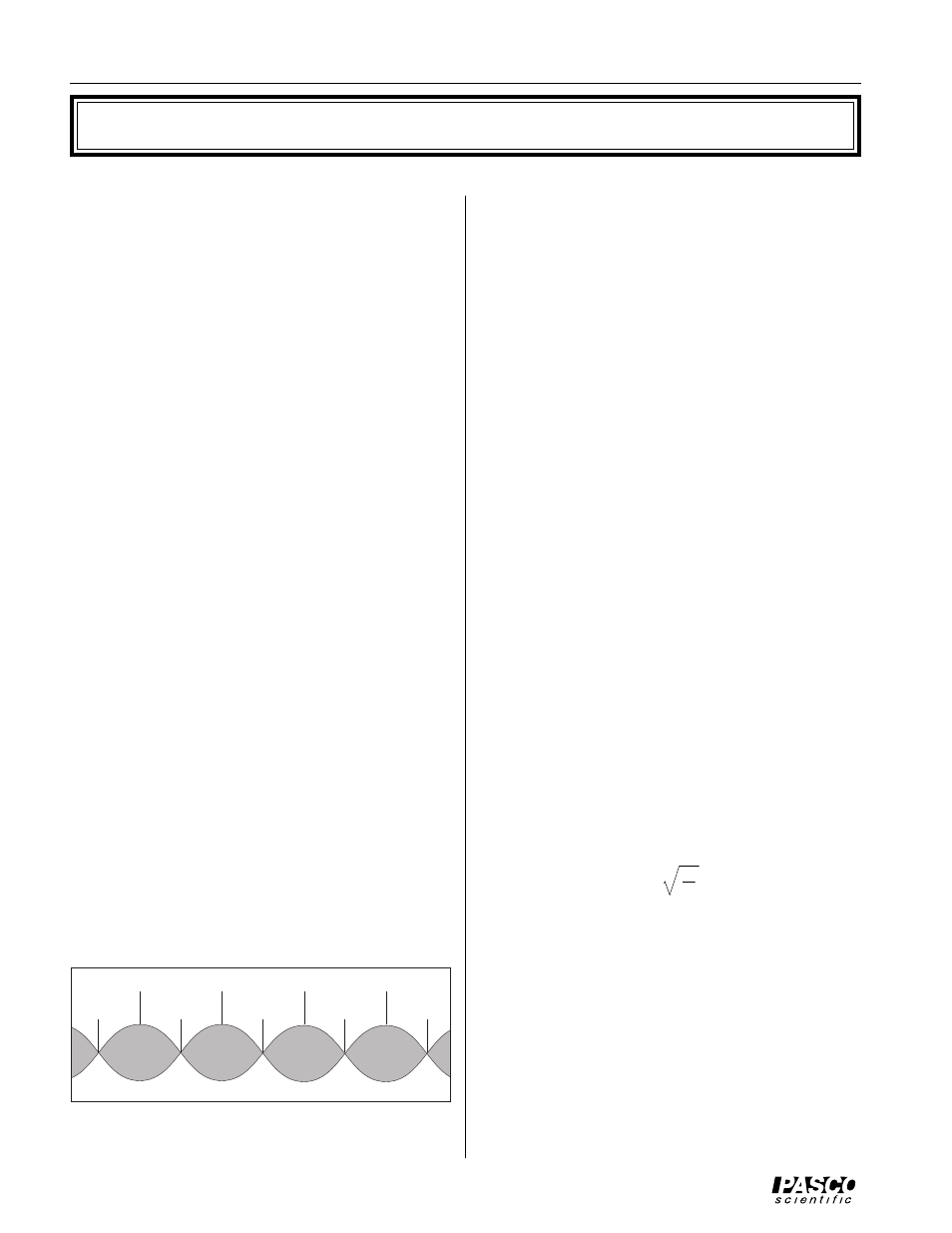
This waveform is called a standing wave because there is
no propagation of the waveform along the string. A time
exposure of the standing wave would show a pattern
something like the one in Figure 8. This pattern is called
the envelope of the standing wave. Each point of the
string oscillates up and down with its amplitude deter-
mined by the envelope. The points of maximum ampli-
tude are called antinodes. The points of zero amplitude
are called nodes.
Node
Antinode
Node
Antinode
Node
Antinode
Node
Antinode
Node
Figure 8 The Envelope of a Standing Wave Pattern