PASCO ME-9833 Physical Pendulum Set - Manual (Page 15)

Physical Pendulum Set Model No. ME-9833
15
®
Experiment 3: Moment of Inertia Based on Period of
Oscillation
Equipment
Use the period of oscillation of a physical pendulum to calculate the moment of inertia. Measure the
moment of inertia and compare the measured value to the calculated value.
Background Information
The period of oscillation, T, of a physical pendulum depends on the moment of inertia about a pivot
point, I
pivot
, the mass, M, and the distance from the pivot point to the center of gravity, L
cg
.
The Parallel Axis Theorem states that the moment of inertia about a pivot point, I
pivot
, is equal to
the sum of the moment of inertia about the center of gravity, I
cg
, and the moment of inertia of the
object as if all its mass were at the center of gravity, ML
2
cg
.
Conversely, the moment of inertia about the center of gravity could be found as follows:
Measurement: Period of Oscillation
Equipment Setup
1. Measure and record the mass M, of the disk.
2. Measure and record the distance, L
cg
, from the
pivot point on the edge of the disk to the center of
the disk.
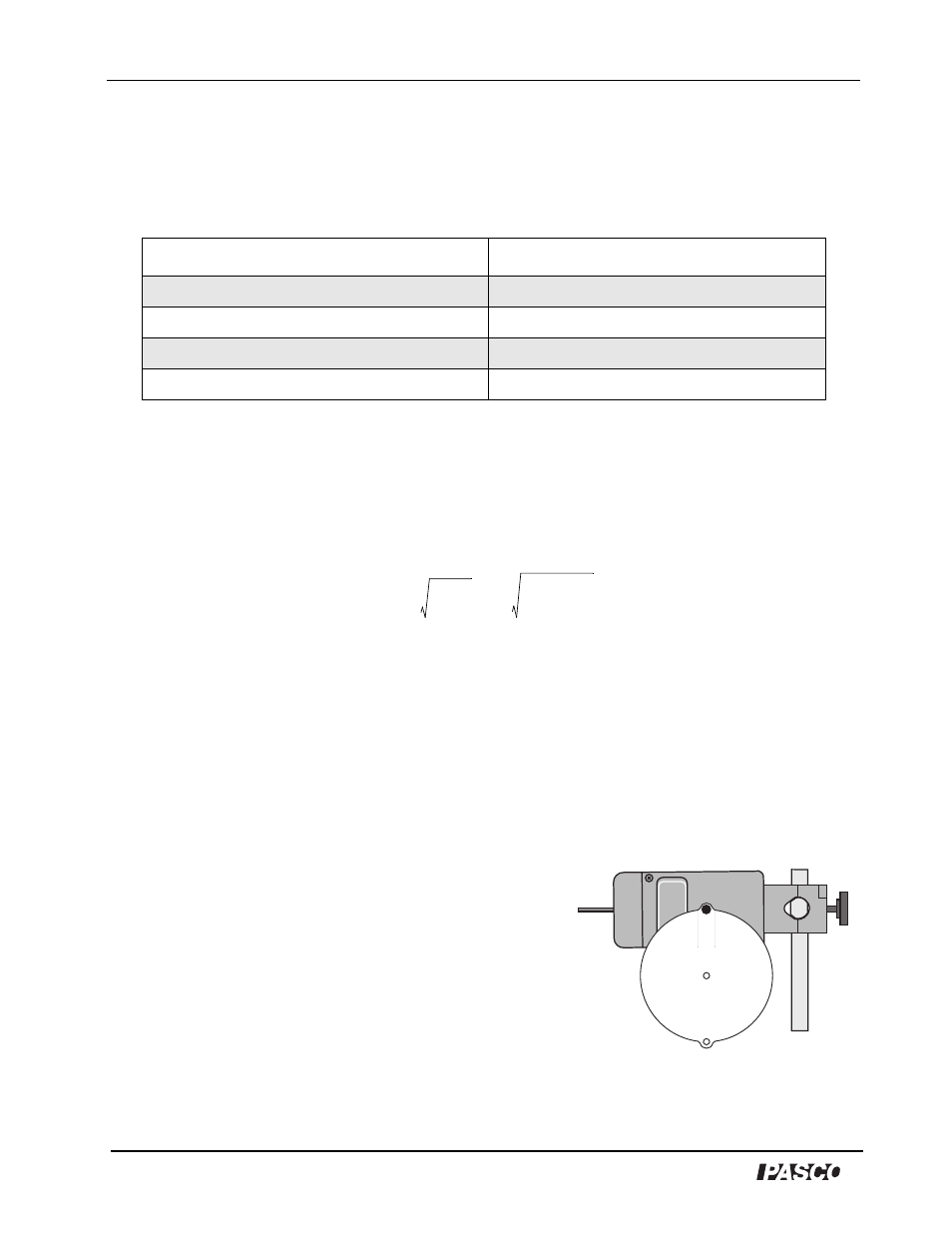
3. Mount the Rotary Motion Sensor on a support rod
so that the shaft of the sensor is horizontal (parallel
to the table).
Item Item
PASCO Interface and DataStudio software Balance
Rotary Motion Sensor Vernier caliper
Physical Pendulum Set Mass and Hanger Set
Base and Support Rod String or thread
T 2 π
I
pivot
MgL
cg
------------------ 2 π
I
cg
ML
2
cg
+
MgL
cg
------------------------------- = =
I
cg
T
2
MgL
cg
4 π 2
------------------------- ML
2
cg
– =
Figure 3-1: Setup