PASCO ME-9341 INTRODUCTORY ROTATIONAL APPARATUS - Manual (Page 29)

012-03051F Introductory Rotational Apparatus
25
Exp 2 – Angular Acceleration - 2
Introduction
In its simplest form, the principles in this lab are very clear, the setup is easy, and the variables are easy to control.
However, in its simplest form, the lab assumes that the mass exerts a constant force of F = mg on the platter.
Since the mass is accelerated along with the platter, the tension (T) on the thread must be less than the mass. An
accurate analysis of the motion must take into account that T, not F, is the force that accelerates the platter. The
following equations and diagram derive the rotational acceleration, a, using T as the force that causes the platter to
rotate.
mg - T = ma = mr
α
τ
= Tr = I
α
a = r
α
→
T = mg - mr
α
τ
= mgr - mr 2 α
= I
α
mgr = I
α
+ mr 2 α
α
= (mgr)/(I + mr
2
)
For large masses or for large values of r, the mr 2 term in the denominator may have a significant impact. For a
mass of 200 grams and a radius of 1.5 cm, the mr
2
term reduces the rotational acceleration only by 0.8%. There-
fore, the decision to neglect this factor does not detract significantly from the final results. However, students can
be given the option of trying to prove the theoretical results as given above.
Alternatives
➀ See Experiment 1: Angular Acceleration - 1.
➁ For a more accurate, but somewhat less straightfor-
ward method, see "Option b" in the note on page 4.
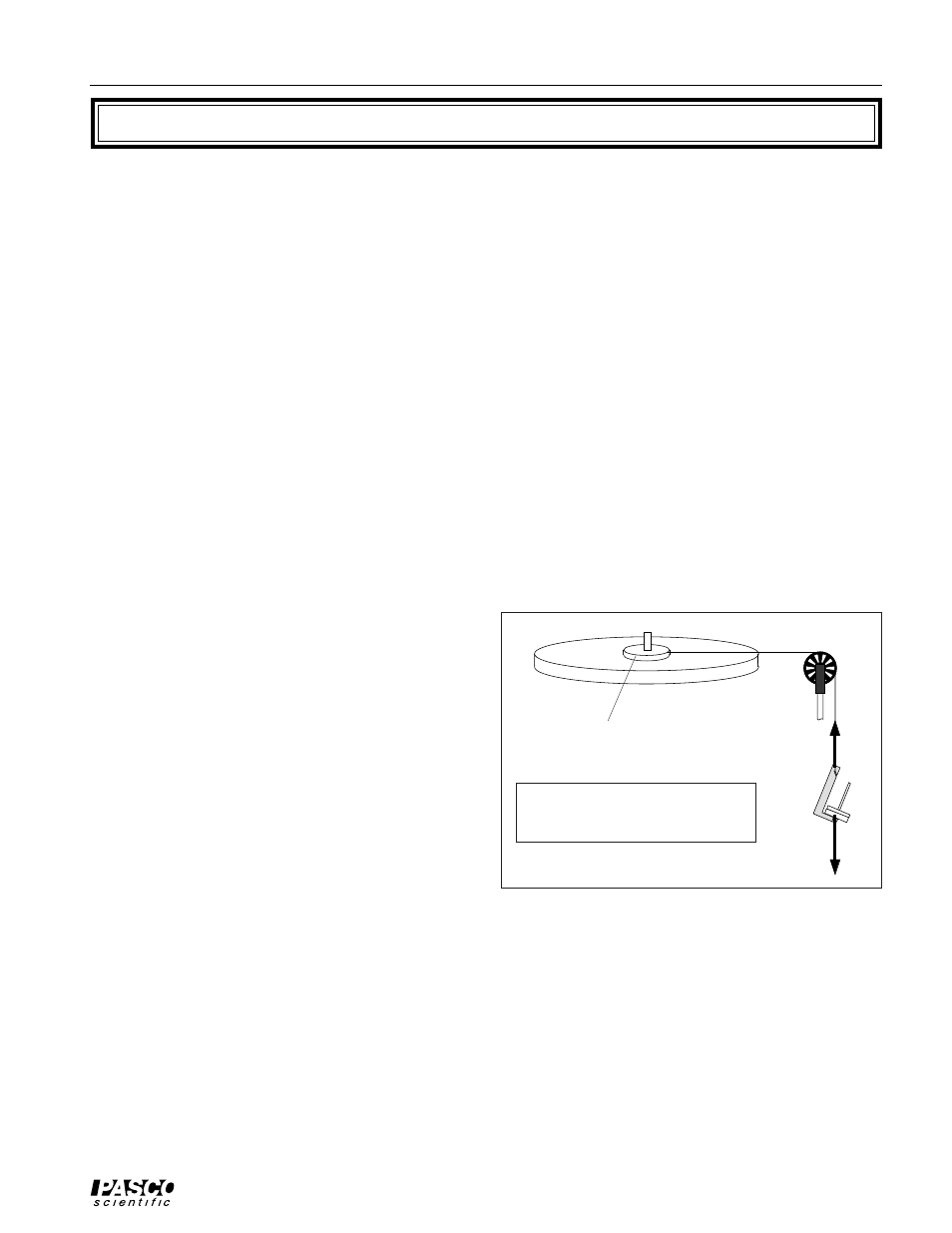
Radius of step pulley
spindle = r
m
T
(Tension)
Experiment 2: Diagram of Relevant Variables
I = Moment of inertia of the platter
= MR
2
for a cylinder.
τ
= Torque = r x T
F = mg
Notes – on Procedure
➂ Using a lighter mass than 40 grams will give good results, as long as it is heavy enough that the frictional
torque may be ignored.
➃ Use a lightweight rubber band to hold the smart pulley against the platter. The pulley should be held with just
enough tension to keep it from slipping; any extra tension will add to the friction of the system.
➈ Using the heavier masses will introduce significant errors due to the linear acceleration of the mass. These er-
rors are negligible when lighter masses are used.