PASCO ME-9341 INTRODUCTORY ROTATIONAL APPARATUS - Manual (Page 16)

12
Introductory Rotational Apparatus 012-03051F
F
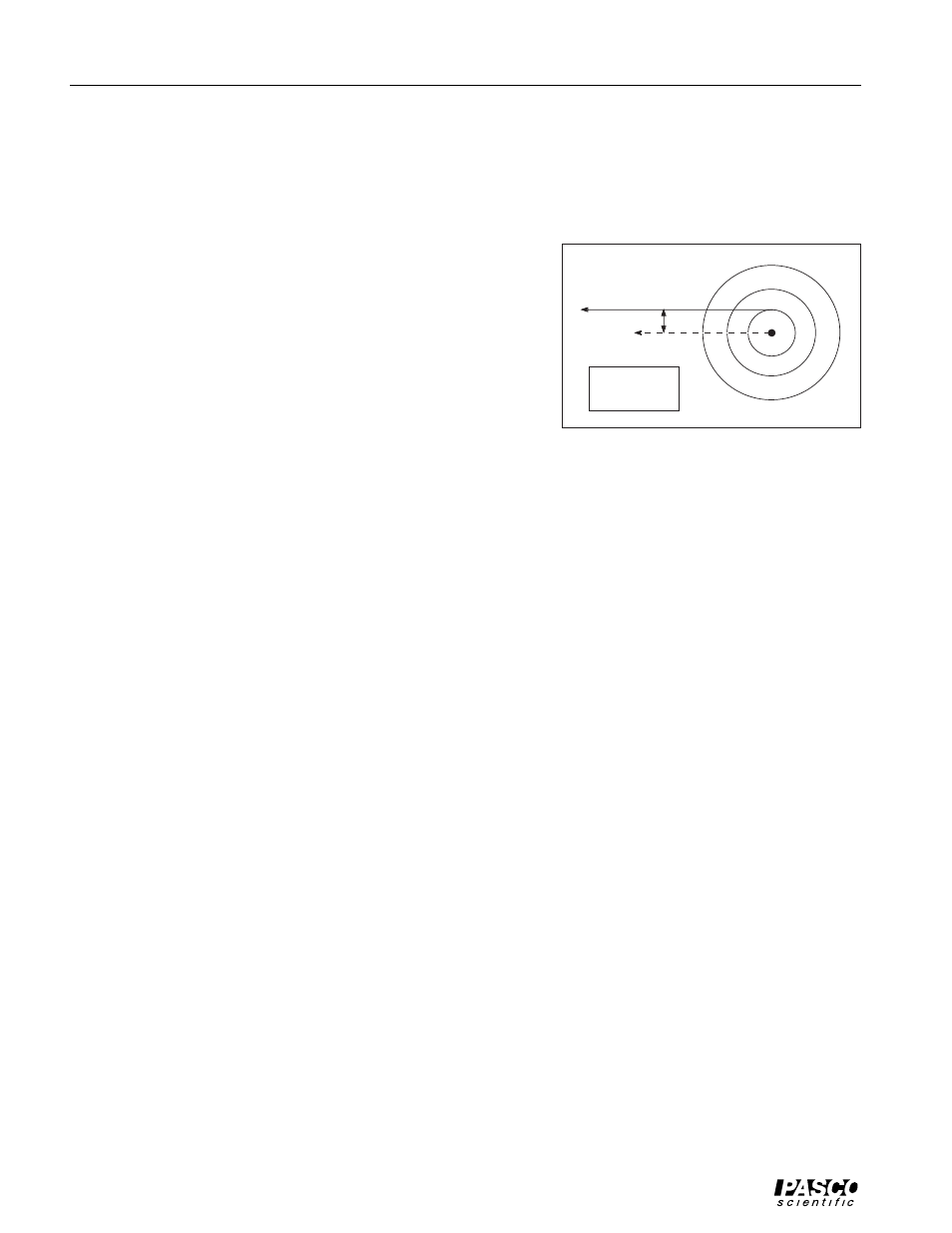
Figure 2.2 The Geometry of Torque
d
⊥
τ
= d
⊥
F
α = τ/Ι
➉ Turn the platter over and place the auxiliary platter on top. Go back to step 4. Use the
smallest spindle and 40 grams total mass. Repeat the measurements using two and then
three auxiliary platters, if you have them. Now try the experiment first with the ring and
then with the steel bar on top of the main platter.
Analysis
Graph angular acceleration versus step pulley radius, given a
constant value for the falling mass. Also graph angular
acceleration versus the value of the falling mass for a con-
stant step pulley radius. The angular acceleration of an object
(a) depends upon the torque (
τ
) applied to it and the moment
of inertia (I) of the object: a =
τ
/I. Torque equals the
applied force times the perpendicular distance from the axis
of rotation to the point of application of the force,
τ
= Fd
⊥
.
In this case, the applied force is the tension, T, in the string.
T must be less than mg, the weight of the falling mass, since
m must experience a net downward force in order to acceler-
ate downward. However, for m less than 40 grams, the step pulley radii are small enough
that the approximation T=mg results in a less than 1% error in the angular acceleration (see
Lab Note on Experiment 2, page 17, for details). Thus, as an approximation, use mg as the
applied force.
In step 8 of the procedure, the applied force (mg) remained constant while the distance, d
⊥
changed (d
⊥
is the step pulley radius). In your first graph, you should see that the angular
acceleration is directly proportional to d
⊥
.
In step 9 of the procedure, d
⊥
remained constant. Therefore, your second graph should
show that angular acceleration is directly proportional to the applied force.
Finally, the angular acceleration is inversely proportional to the moment of inertia, given a
constant torque. The moment of inertia of an object depends on its mass and on how that
mass is distributed. In the first part of step 10, you increased the mass but kept the distribu-
tion the same. What affect did the increased mass have on the acceleration? What affect
did it have on the moment of inertia?
The platter, the ring, and the bar have approximately the same mass. Based on your accel-
eration data, rank them from greatest to least in terms of their moments of inertia. Be
prepared to explain your reasoning. Do your results agree with theory?
Report
Your report should include Purpose, Procedure, Data, and Discussion. Your Discussion
should include your analysis. Compare rotational dynamics with linear dynamics in your
Discussion.
Beyond
In the Analysis above, the effect of the acceleration of the falling mass was neglected. If
your instructor wishes, include this effect and analyze this more complex situation in your
discussion and analysis.