PASCO AP-8215A Gravitational Torsion Balance - Manual (Page 14)

®
G r a v i t a t i o n a l T o r s i o n B a l a n c e M E T H O D I : M e a s u r e m e n t b y F i n a l D e f l e c t i o n
10
5. Use a stop watch to determine the time required for one period of oscillation (T). For greater accuracy,
include several periods, and then find the average time required for one period of oscillation.
Note: The accuracy of this period value (T) is very important, since the T is squared in the calculation of G.
6. Wait until the oscillations stop, and record the resting equilibrium point (S
2
).
Analysis
1. Use your results and equation 1.9 to determine the value of G.
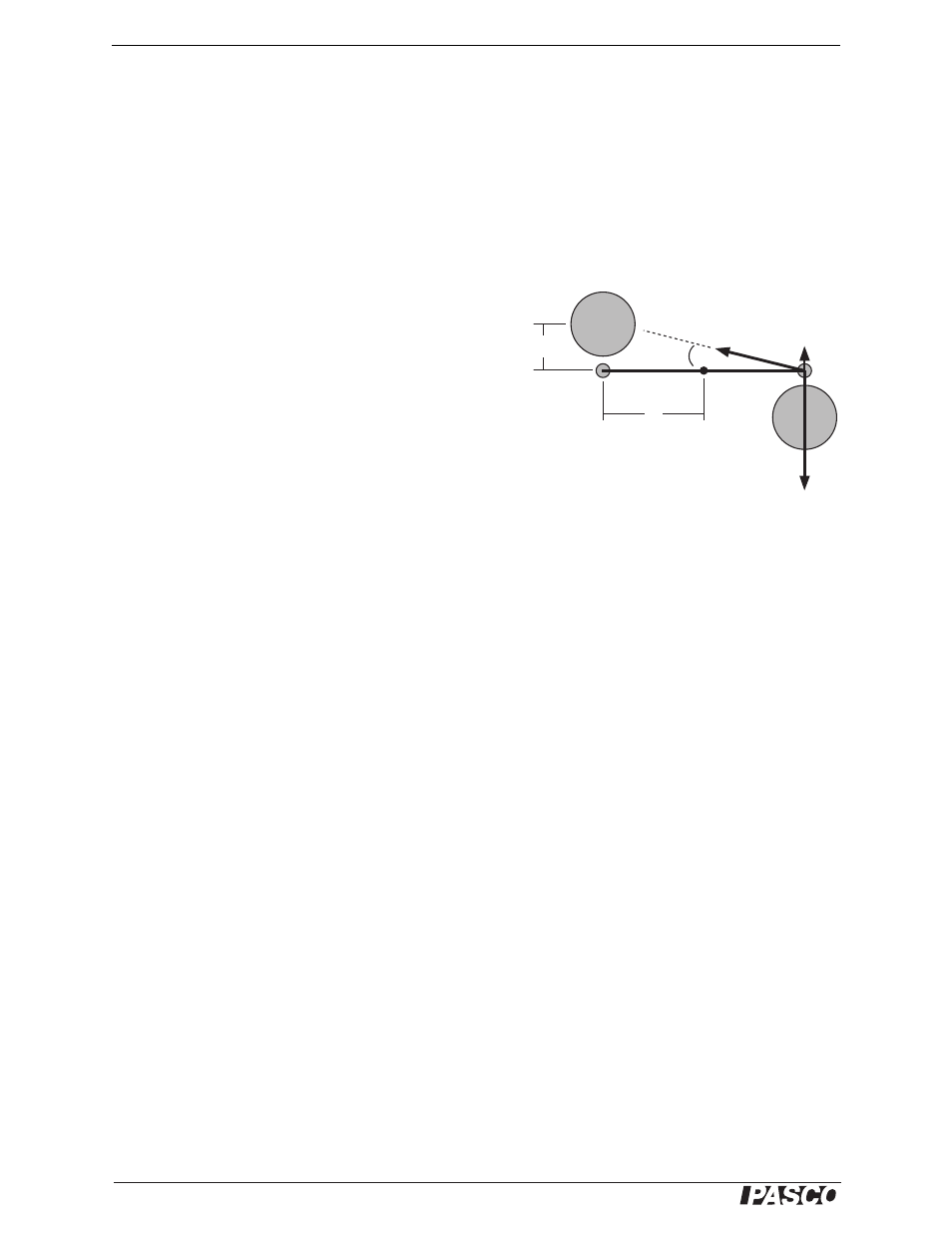
The value calculated in step 2 is subject to the following sys-
tematic error. The small sphere is attracted not only to its
neighboring large sphere, but also to the more distant large
sphere, though with a much smaller force. The geometry for
this second force is shown in Figure 17 (the vector arrows
shown are not proportional to the actual forces).
From Figure 17,
The force, F
0
is given by the gravitational law, which trans-
lates, in this case, to:
and has a component ƒ that is opposite to the direction of the force F :
This equation defines a dimensionless parameter,  , that is equal to the ratio of the magnitude of ƒ to that of F.
Using the equation F = Gm
1
m
2
/b
2
, it can be determined that:
From Figure 17, F
net
= F - f = F -  F = F(1 -  )
where F
net
is the value of the force acting on each small sphere from both large masses, and F is the force of
attraction to the nearest large mass only.
Similarly, G = G
0
(1 -  )
where G is your experimentally determined value for the gravitational constant, and G
0
is corrected to account
for the systematic error.
Finally, G
0
= G/(1 -  )
Use this equation with equation 1.9 to adjust your measured value.
Φ
d
b
F
0
F
f
Figure 17: Correcting the
measured value of G
f F
0
 sin =
F
0
Gm
2
m
1
b
2
4d
2
+  
------------------------- =
f
Gm
2
m
1
b
b
2
4d
2
+   b
2
4d
2
+  
1
2
---
------------------------------------------------------ F = =

b
3
b
2
4d
2
+  
3
2
---
---------------------------- =