PASCO AP-8215A Gravitational Torsion Balance User Manual
Page 12
®
G r a v i t a t i o n a l T o r s i o n B a l a n c e
M E T H O D I : M e a s u r e m e n t b y F i n a l D e f l e c t i o n
8
Since the system is in equilibrium, the twisted torsion
band must be supplying an equal and opposite torque.
This torque (
band
) is equal to the torsion constant for the
band (
) times the angle through which it is twisted (),
or:
Combining equations 1.1, 1.2, and 1.3, and taking into
account that
grav
= –
band
, gives:
Rearranging this equation gives an expression for G:
To determine the values of
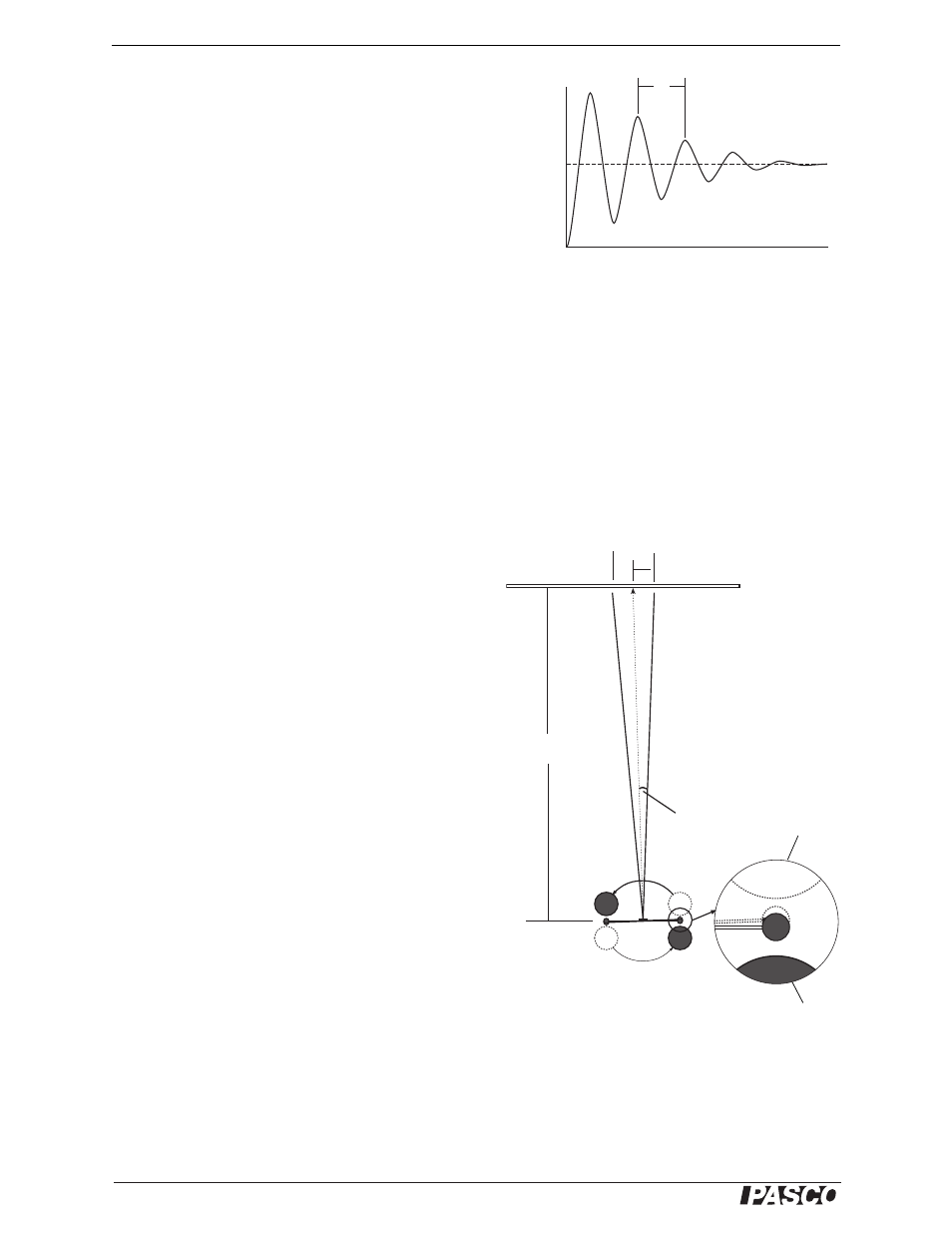
and — the only unknowns in equation 1.4 — it is necessary to observe the oscil-
lations of the small mass system when the equilibrium is disturbed. To disturb the equilibrium (from S
1
), the
swivel support is rotated so the large masses are moved to Position II. The system will then oscillate until it
finally slows down and comes to rest at a new equilibrium position (S
2
) (Figure 14).
At the new equilibrium position S
2
, the torsion wire will
still be twisted through an angle
, but in the opposite
direction of its twist in Position I, so the total change in
angle is equal to 2
. Taking into account that the angle is
also doubled upon reflection from the mirror (Figure 15):
S = S
2
– S
1
,
or
The torsion constant can be determined by observing the
period (T) of the oscillations, and then using the equa-
tion:
where I is the moment of inertia of the small mass sys-
tem.
The moment of inertia for the mirror and support system
for the small masses is negligibly small compared to that
of the masses themselves, so the total inertia can be
expressed as:
T
20
60
S
(cm)
Time
(min)
s
2
s
1
Figure 14: Graph of Small Mass Oscillations
band
1.3
–
=
2dGm
1
m
2
b
2
-------------------------
=
G
b
2
2dm
1
m
2
---------------------
1.4
=
S
1
S
2
ΔS
2
θ
L
Figure 15: Diagram of the experiment
showing the optical lever.s
Position I
Position II
2
2
tan
»
S
2L
-------
=
4
S
L
-------
=
S
4L
-------
1 5
=
T
2
4
2
I
-----------
1 6
=
I
2m
2
d
2
2
5
---r
2
+
1.7
=
