Position i, Procedure – PASCO AP-8215A Gravitational Torsion Balance User Manual
Page 13
®
M o d e l N o . A P - 8 2 1 5 A
M E T H O D I : M e a s u r e m e n t b y F i n a l D e f l e c t i o n
9
Therefore:
Substituting equations 1.5 and 1.8 into equation 1.4 gives:
All the variables on the right side of equation 1.9 are known or measurable:
r = 9.55 mm
d = 50 mm
b = 42.2 mm
m
1
= 1.5 kg
L = (Measure as in step 1 of the setup.)
By measuring the total deflection of the light spot (
S) and the period of oscillation (T), the value of G can there-
fore be determined.
Procedure
1. Once the steps for leveling, aligning, and setup have been
completed (with the large masses in Position I), allow the pen-
dulum to stop oscillating.
2. Turn on the laser and observe the Position I end point of the
balance for several minutes to be sure the system is at equilib-
rium. Record the Position I end point (S
1
) as accurately as
possible, and indicate any variation over time as part of your
margin of error in the measurement.
3. Carefully rotate the swivel support so that the large masses are
moved to Position II. The spheres should be just touching the
case, but take care to avoid knocking the case and disturbing
the system.
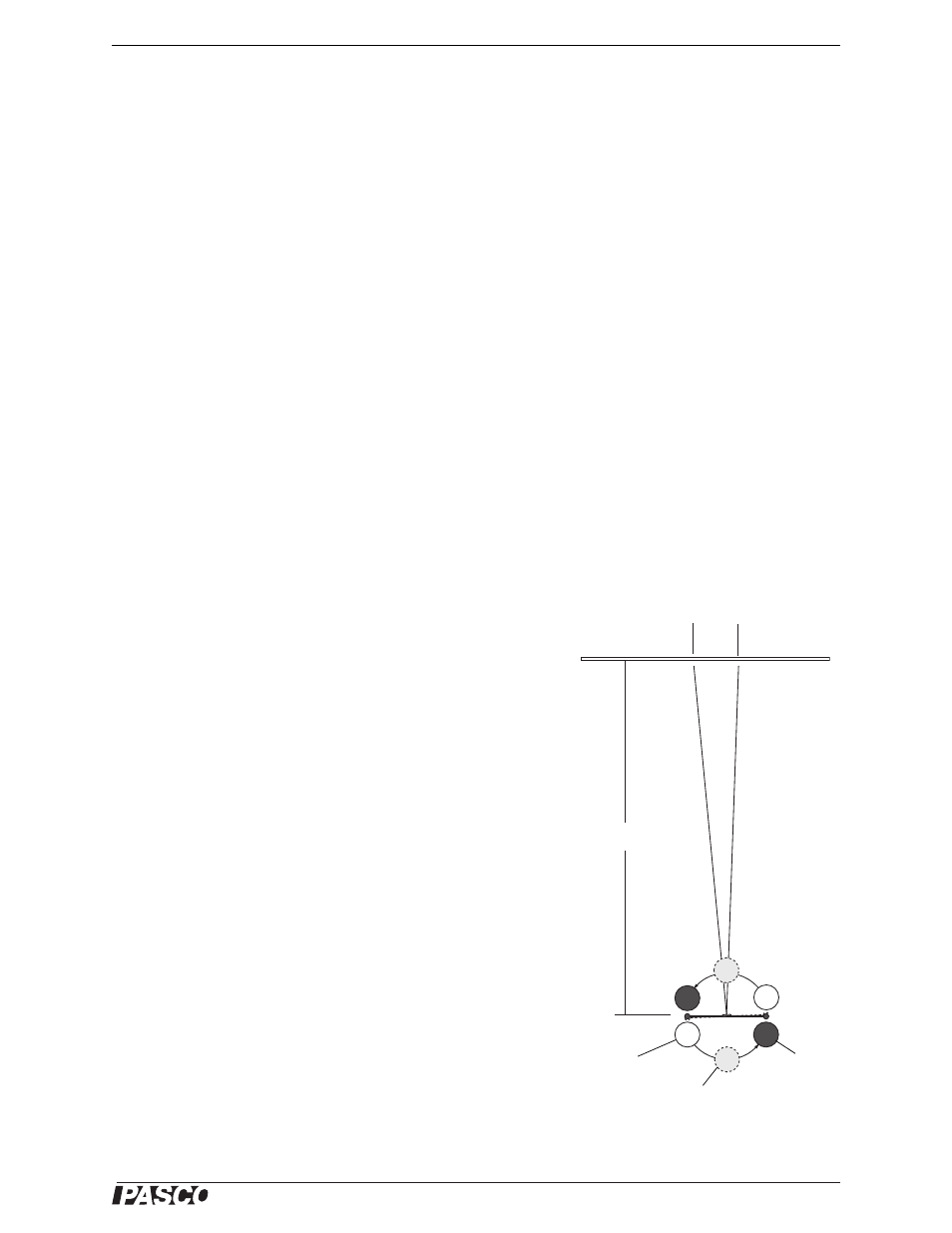
Note: You can reduce the amount of time the pendulum requires to
move to equilibrium by moving the large masses in a two-step pro-
cess: first move the large masses and support to an intermediate
position that is in the midpoint of the total arc (Figure 16), and
wait until the light beam has moved as far as it will go in the
period; then move the sphere across the second half of the arc until
the large mass support just touches the case. Use a slow, smooth
motion, and avoid hitting the case when moving the mass support.
4. Immediately after rotating the swivel support, observe the
light spot and record its position (S
1
).
8
2
m
2
d
2
2
5
---r
2
+
T
2
--------------------
1.8
=
G
2
Sb
2
d
2
2
5
---r
2
+
T
2
m
1
Ld
--------------------
1.9
=
S
1
S
2
L
Position I
Position II
Intermediate
position
Figure 16: Two-step process of moving the
large masses to reduce the time required to
stop oscillating.
