PASCO AP-8215A Gravitational Torsion Balance - Manual (Page 11)

®
M o d e l N o . A P - 8 2 1 5 A M e a s u r i n g t h e G r a v i t a t i o n a l C o n s t a n t
7
Measuring the Gravitational Constant
Overview of the Experiment
The gravitational attraction between a 15 gram mass and a 1.5 kg mass when their centers are separated by a dis-
tance of approximately 42.2 mm (a situation similar to that of the Gravitational Torsion Balance ) is about
7 x 10
-10
newtons. If this doesn’t seem like a small quantity to measure, consider that the weight of the small
mass is more than two hundred million times this amount.
The enormous strength of the Earth's attraction for the small masses, in comparison with their attraction for the
large masses, is what originally made the measurement of the gravitational constant such a difficult task. The tor-
sion balance (invented by Charles Coulomb) provides a means of negating the otherwise overwhelming effects
of the Earth's attraction in this experiment. It also provides a force delicate enough to counterbalance the tiny
gravitational force that exists between the large and small masses. This force is provided by twisting a very thin
beryllium copper ribbon.
The large masses are first arranged in Position I, as shown in Figure 12, and
the balance is allowed to come to equilibrium. The swivel support that holds
the large masses is then rotated, so the large masses are moved to Position
II, forcing the system into disequilibrium. The resulting oscillatory rotation
of the system is then observed by watching the movement of the light spot
on the scale, as the light beam is deflected by the mirror.
Any of three methods can be used to determine the gravitational constant,
G, from the motion of the small masses. In Method I, the final deflection
method, the motion is allowed to come to resting equilibrium—a process
that requires several hours—and the result is accurate to within approxi-
mately 5%. In Method II, the equilibrium method, the experiment takes 90
minutes or more and produces an accuracy of approximately 5% when graphical analysis is used in the proce-
dure. In Method III, the acceleration method, the motion is observed for only 5 minutes, and the result is accurate
to within approximately 15%.
METHOD I: Measurement by Final Deflection
Setup Time: ~ 45 minutes; Experiment Time: several hours
Accuracy: ~ 5%
Theory
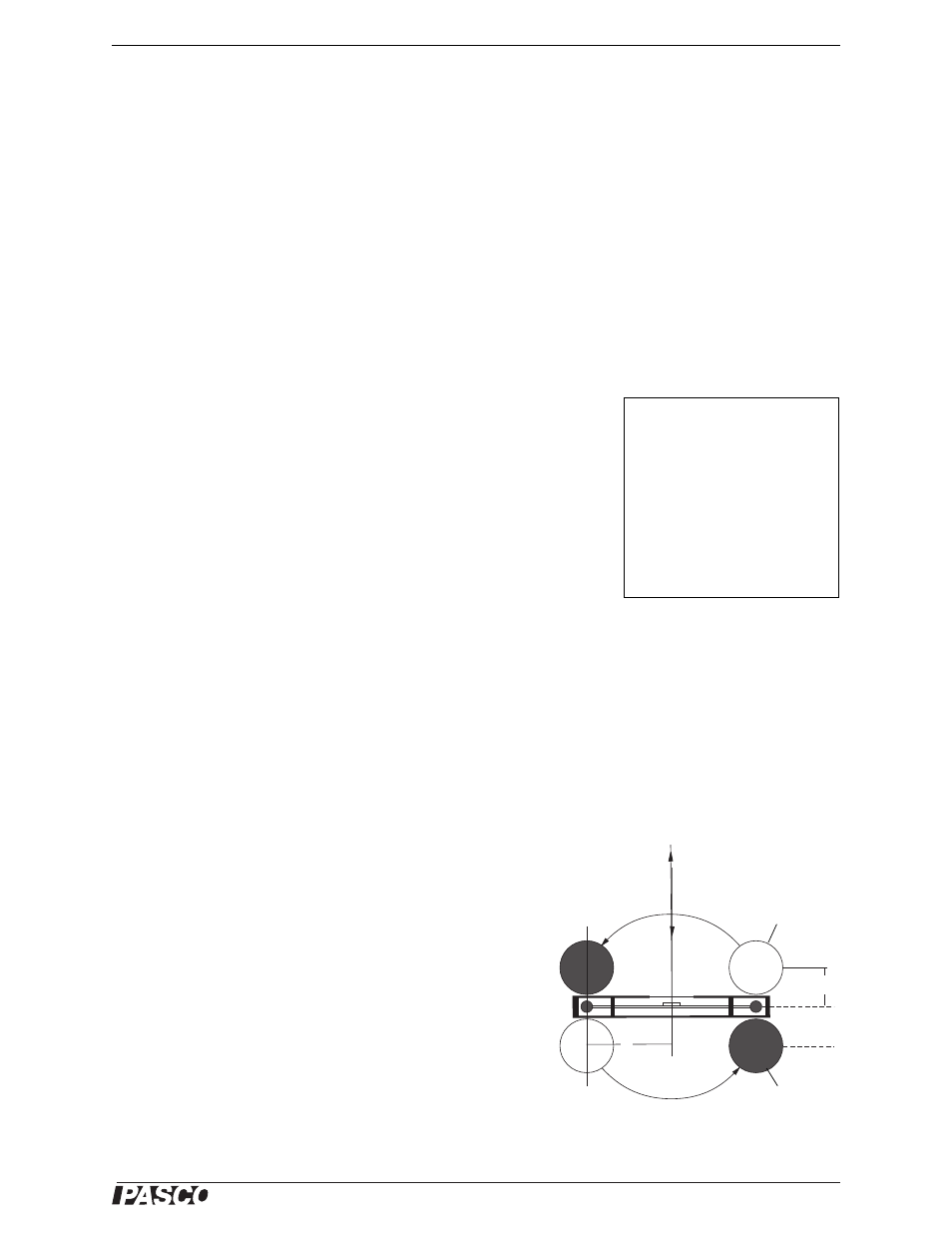
With the large masses in Position I (Figure 13), the gravitational
attraction, F, between each small mass (m
2
) and its neighboring
large mass (m
1
) is given by the law of universal gravitation:
where b is the distance between the centers of the two
masses.
The gravitational attraction between the two small masses and
their neighboring large masses produces a net torque (

grav
) on
the system:
where d is the length of the lever arm of the pendulum bob cross-
piece.
Note: 5% accuracy is possible in
Method I if the experiment is set up
on a sturdy table in an isolated loca-
tion where it will not be disturbed by
vibration or air movement.
Note: 5% accuracy is possible in
Method II if the resting equilibrium
points are determined using a
graphical analysis program.
d
b
Large Masses:
Position I
Large Masses:
Position II
Figure 13: Origin of
variables b and d
F G
m
1
m
2
b
2
-------------- 1.1   =

grav
2Fd 1.2   =