3B Scientific Pohl's Torsion Pendulum User Manual

Page 14

5. Exemples d’expériences

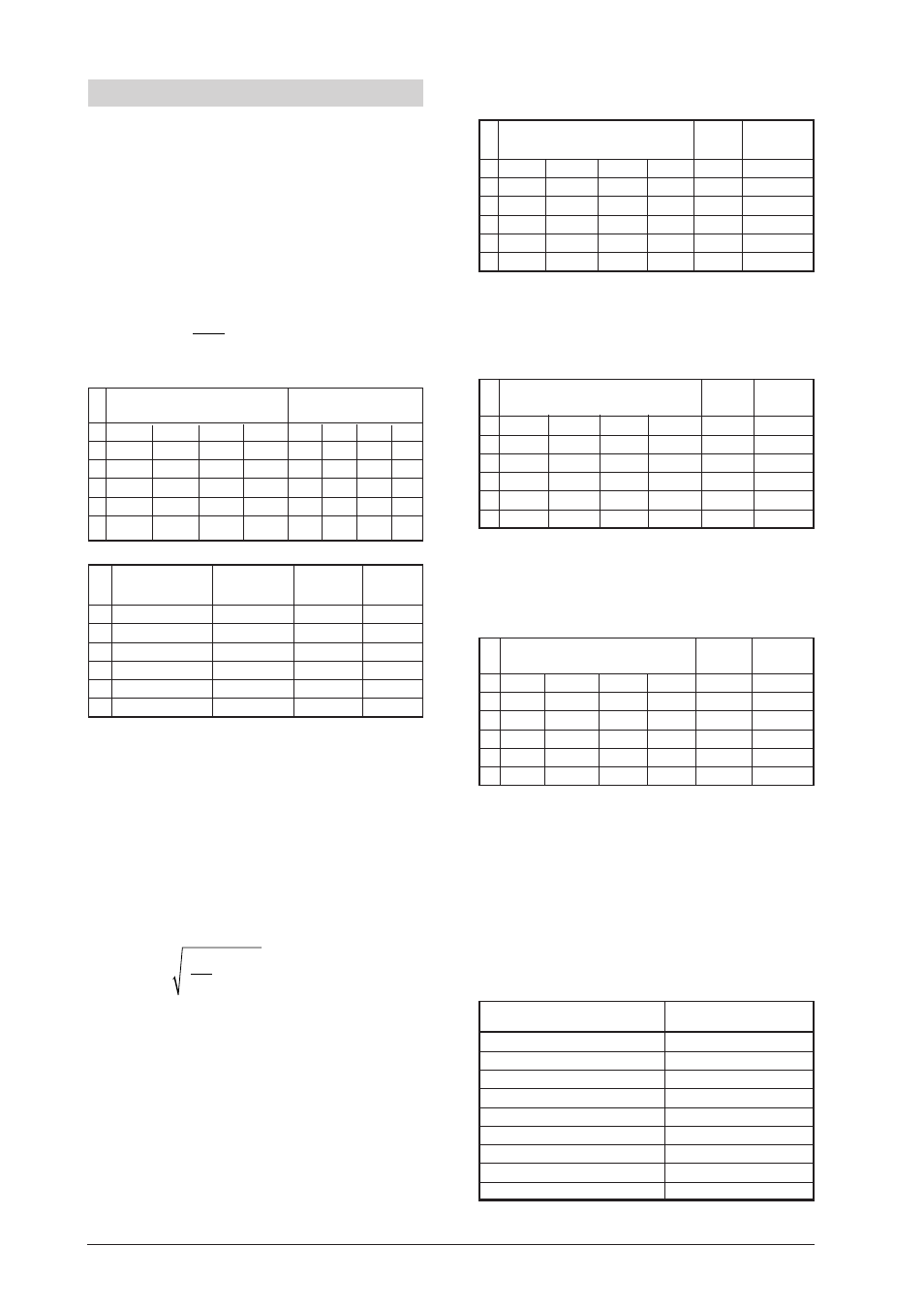
5.1 Oscillation tournante amortie libre
• Pour définir le décrément logarithmique Λ, mesu-

rer et déterminer les amplitudes en plusieurs pas-
sages. Pour cela, au cours de deux séries de mesu-
res, lire les déviations du pendule tournant sur la
graduation à gauche et à droite.

• Le point de départ du corps du pendule était 15 ou

–15 sur la graduation. Cinq déviations ont été lues.

• A partir du rapport des amplitudes, on obtient Λ à

l’aide de la formule suivante :

Λ =













n+1

–

0 –15

–15

1 –14,8 –14,8 –14,8 –14,8 14,8 14,8 14,8 14,8
2 –14,4 –14,6 –14,4 –14,6 14,4 14,4 14,6 14,4
3 –14,2 –14,4 –14,0 –14,2 14,0 14,2 14,2 14,0
4 –13,8 –14,0 –13,6 –14,0 13,8 13,8 14,0 13,8
5 –13,6 –13,8 –13,4 –13,6 13,4 13,4 13,6 13,6

–

Λ –

Λ +

–15

–14,8

14,8

0,013

–14,5

14,5

0,02

–14,2

14,1

0,021

0,028

–13,8

13,8

0,028

0,022

–13,6

13,5

0,015

0,022

• La valeur déterminée pour Λ est Λ = 0,0202.

• Pour la durée d’oscillation T du pendule, t = n · T.

Pour cela, mesurer avec un chronomètre la durée
de 10 oscillations et calculer T.

T = 1,9 s

• Ces valeurs permettent de déterminer la constante

d’amortissement

δ avec δ = Λ / T.

δ = 0,0106 s

–1

• Pour la fréquence propre ω, on a l’équation

= 






−

ω = 3,307 Hz

5.2 Oscillation tournante amortie libre
• Pour déterminer la constante d’amortissement δ

en fonction de l’intensité

Ι par l’électro-aimant, la

même expérience a été réalisée avec un frein à cou-
rants de Foucault à

Ι = 0,2 A, 0,4 A et 0,6 A.

ΙΙΙΙΙ = 0,2 A

–

Λ –

0 –15

–15

1 –13,6

–13,8

–13,6 –13,7

0,0906

2 –12,6

–12,8

–12,6

–12,4 –12,6

0,13

3 –11,4

–11,8

–11,6

–11,4 –11,5

0,0913

4 –10,4

–10,6

–10,4

–10,4 –10,5

0,0909

5 9,2

–9,6

–9,6 –9,5

0,1

• Avec T = 1,9 s et la moyenne Λ = 0,1006, on ob-

tient la constante d’amortissement :

δ = 0,053 s

–1

ΙΙΙΙΙ = 0,4 A

–

Λ –

–15

–11,8 –11,8

–11,6 –11,6

–11,7

0,248

–9,2

–9,0

–9,2

–9,1

0,25

–7,2

–7,0

–7,1

0,248

–5,8

–5,6

–5,4

–5,2

–5,5

0,25

–4,2

–4,0

–4,1

0,29

• Avec T = 1,9 s et la moyenne Λ = 0,257, on obtient

la constante d’amortissement :

δ = 0,135 s

–1

ΙΙΙΙΙ = 0,6 A

–

Λ –

–15

–9,2

–9,4

–9,2

–9,3

0,478

–5,4

–5,2

–5,6

–5,8

–5,5

0,525

–3,2

–3,4

–3,3

0,51

–1,6

–1,8

0,606

–0,8

0,81

• Avec T = 1,9 s et la moyenne Λ = 0,5858 on obtient

la constante d’amortissement :

δ = 0,308 s

–1

5.3 Oscillation tournante forcée
• Pour déterminer l’amplitude de l’oscillation en

fonction de la fréquence de l’excitateur et de la ten-
sion d’alimentation, lire la déviation maximale du
corps du pendule.

T = 1,9 s

Tension moteur V

0,8

1,1

1,2

1,6

3,3

7,6

20,0

16,8

1,6

1,1