Cannot reach 25 pa factors – Retrotec DucTester 200 Series Residential Applications User Manual
Page 76
Page 76 of 91
©Retrotec Inc. 2015
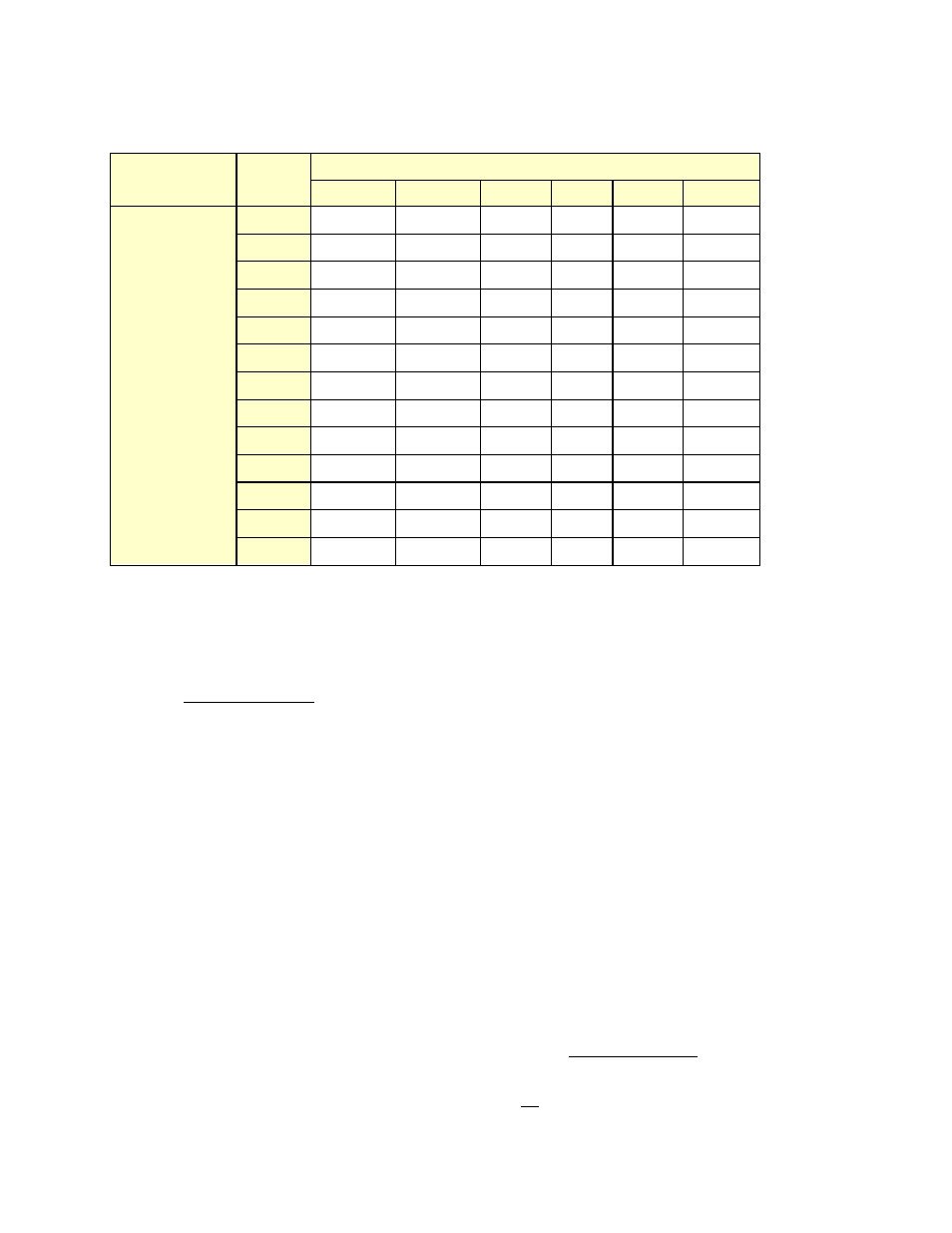
If the “n” value on the gauge is set to 0.60 and the enclosure “n” is different, a small error, as shown in
Table 13 will result if the
[@ Pressure]
function is used at the Achieved Pressure to estimate a result at
50 Pa.
Table 13: Errors in Estimated Flow at 50 Pa if gauge "n" = 0.60 differs from actual n
Assumed n = 0.6
Actual Flow Exponent (n) of Enclosure
0.50
0.55
0.60
0.65
0.70
0.75
Achieved
Pressure (Pa)
10
-14.9%
-7.7%
0.0%
8.4%
17.5%
27.3%
15
-11.3%
-5.8%
0.0%
6.2%
12.8%
19.8%
20
-8.8%
-4.5%
0.0%
4.7%
9.6%
14.7%
25
-6.7%
-3.4%
0.0%
3.5%
7.2%
11.0%
30
-5.0%
-2.5%
0.0%
2.6%
5.2%
8.0%
35
-3.5%
-1.8%
0.0%
1.8%
3.6%
5.5%
40
-2.2%
-1.1%
0.0%
1.1%
2.3%
3.4%
45
-1.0%
-0.5%
0.0%
0.5%
1.1%
1.6%
50
0.0%
0.0%
0.0%
0.0%
0.0%
0.0%
55
1.0%
0.5%
0.0%
-0.5%
-0.9%
-1.4%
60
1.8%
0.9%
0.0%
-0.9%
-1.8%
-2.7%
65
2.7%
1.3%
0.0%
-1.3%
-2.6%
-3.9%
70
3.4%
1.7%
0.0%
-1.7%
-3.3%
-4.9%
Achieved pressure is the actual maximum pressure achieved in the enclosure (ducts in this case) during
the test.
Error = (
Pressure of Interest
Achieved Pressure
)
(Actual n−Assumed n)
In the tables, the Pressure of Interest is 50Pa, and Assumed n is 0.65 or 0.60
The actual flow exponent n for an enclosure can be calculated by measuring enclosure leakage at
multiple pressure differences, from 10 to 50 Pa, and determining the slope of the line on the graph of
pressure versus flow which will be linear if graphed on a log-log scale, and the slope will be n.
Cannot Reach 25 Pa Factors
If you have a situation where you cannot reach the required 25 Pa during the test, there is a way to
estimate the flow at that pressure based on the measured pressure and flow you did achieve. This is the
procedure the gauge uses for extrapolating the flow at the required pressure when you use the
[@
Pressure]
key. The following equation describes the relationship between the flow at the required
pressure of 25 Pa and the actual measured flow at the measured pressure:
Flow at 25 Pa = (Flow at measured pressure) ∗ (
25 Pa
measured pressure
)
n
CFM
25
= CFM
P
∗ (
25
P
)
n
