3 quarter bridge strain with dummy gage – Campbell Scientific 4WFBS120, 4WFBS350, 4WFBS1K 4 Wire Full Bridge Terminal Input Modules User Manual
Page 24
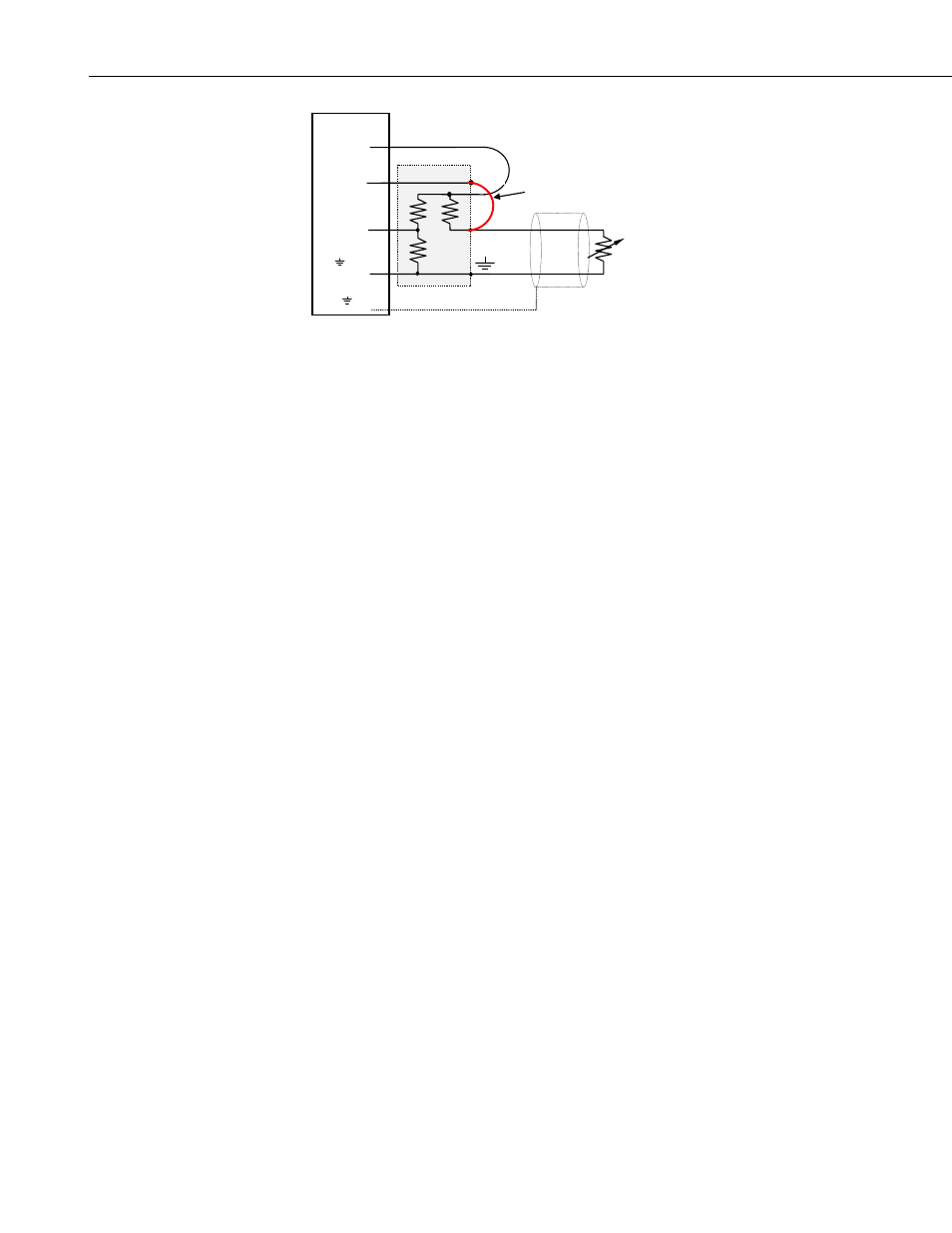
4WFBS120, 4WFBS350, 4WFBS1K 4 Wire Full Bridge Terminal Input Modules (TIM)
Shield
18
H
L
G
Datalogger
Vx
H
L
or AG
H
or G
Jumper Wire
R
1
R
2
R
D
Gauge
4
7
3
4
2
93
.
3
25
.
3
05
.
0
15
.
1
95
.
2
T
E
T
E
T
T
TO
−
−
−
+
−
+
−
=
με
FIGURE 4.2-2. Wiring for 2-wire gauges
4.2.2 Two Wire ¼ Bridge use with Multiplexers and Equations
The equations to resolve the strain, programming of the logger, and methods of
using with multiplexers are the same as those covered in Section 4.1 for the 3-
Wire Strain gauge. The only variance is the wiring of the gage to the TIM.
4.3 Quarter Bridge Strain with Dummy Gage
An undesirable property of strain gauges is that of resistance change with
changes in temperature. This is true even for the self-temperature
compensating strain gages on the market today. Supplied with each package of
strain gages are graphs and equations for the variance in the output of the strain
gage due to thermal changes (referred to as thermal output or apparent strain)
and for the variation of the gage factor with temperature. These graphs are
based on the assumption that the gages are mounted on a material with the
given thermal coefficient of expansion (TCE). The TCE value is included in
the gage type nomenclature. Following are some typical equations supplied.
Equation 4.3.1 is used to calculate the thermal output variance (
µε
TO
) with the
result in μStrain. Equation 4.3.2 is used to determine the change in the gauge
factor (GF) due to temperature changes. Both are based on temperature in
degrees Celsius (T).
4.3.1
(
)
raw
raw
adj
GF
T
E
GF
GF
24
40
.
1
4
−
×
+
=
−
4.3.2
As an example, let us assume we use a gauge with a GF of 2.00 in a test that
started at 24°C and 0
μStrain, and ended at 50°C and a recorded strain value of
1000 μStrain. The thermal output strain,
µε
TO
, at 50°C would be -29.3
μStrain. The error in the gage factor would be 0.364% with a resultant GF
adj
of
2.007. The corrected strain would be 967 μStrain:
(
)
007
.
2
/
000
.
2
3
.
29
1000
με
=
−
με
με
×
cor
4.3.3
The uncorrected value had an error of approximately 3.3%. And if the ending
strain would have been 100 μStrain instead of 1000 μStrain, the error would
have been around 30%.
