LumaSense Technologies MCS640 Manual - Manual (Page 17)

13
Section 4 Principles of Thermal Imaging
4.3 Blackbody Radiation
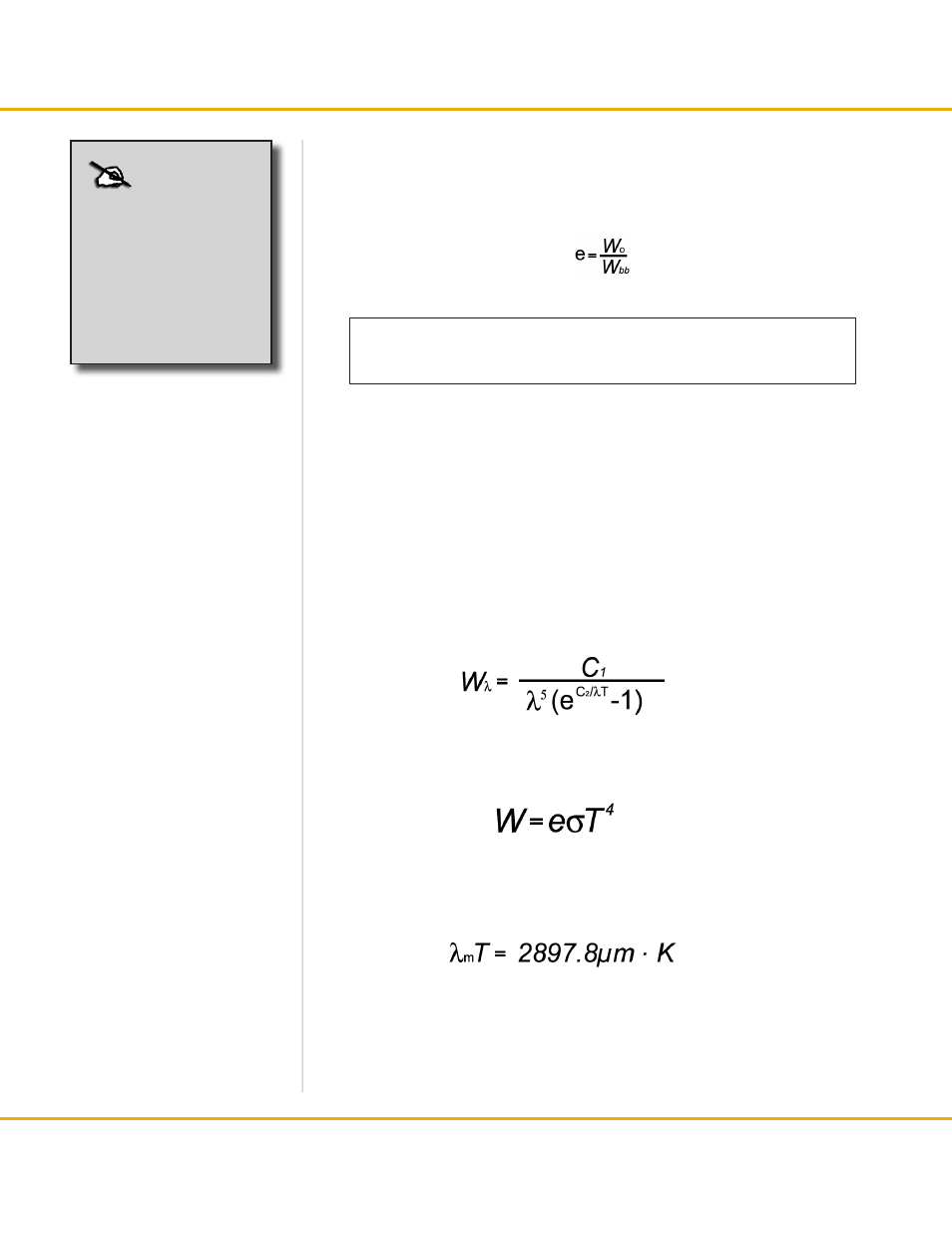
The emissivity of a body is defined formally by the equation below as the ratio of
the radiant energy emitted by the body to the radiation, which would be emitted by a
blackbody at the same temperature.
Where,
W
o
= total radiant energy emitted by a body at a given temperature T.
W
bb
= total radiant energy emitted by a blackbody at the same temperature T.
If all energy falling on an object were absorbed (no transmission or reflection), the
absorptivity would equal to 1. At a steady temperature, all the energy absorbed could be
re-radiated (emitted) so that the emissivity of such a body would equal 1. Therefore in a
blackbody,
absorptivity = emissivity = 1
Practical real life objects do not behave exactly as this ideal, but as described with
transmissivity and reflectivity,
absorptivity + transmissivity + reflectivity = 1
Energy radiated from the blackbody is described as follows [“Planck’s Law”.]
(1)
In order to obtain total radiant emittance of the blackbody, integrate the equation (1)
through all wavelengths (0 to infinity). The result is as follows and is called “Stefan-
Bolzmann equation.”
(2)
The temperature of blackbody can be obtained directly from the radiant energy of the
blackbody by this equation. In order to find out the wavelength on the maximum spectral
radiant emittance, differentiate Planck’s law and take the value to 0.
(3)
This equation is called “Wien’s displacement law”.
Note:
A blackbody is a theoreti-
cal surface, which absorbs
and re-radiates all the IR
energy it receives. It does
not reflect or transmit any
IR energy. Perfect black-
body surfaces do not exist
in nature.
planck’s law
stefan Bolzmann’s equation
Wien’s displacement law