Atec Yokogawa-WT1800 - Manual (Page 13)

Explanations Explanations Explanations
AC signals are repeatedly changing waveforms in terms of instantaneous values. An averaging
calculation by the repeated periods is required to be performed to measure the power value of
the AC signals. The WT1800 uses an ASSP method to perform averaging processing by the
periods for the instantaneous data measured at an approximately 2 MS/s rate to obtain the
measurement value.
ASSP Method
An ASSP (Average for the Synchronous Source Period) method is used to calculate the
measurement value by performing calculation processing for the sampling data within the data
update period (with the exception of the integrated power value WP and integrated current value
q in the DC mode). This method uses a frequency measurement circuit to detect the period of
the input signal set in the synchronous source and performs calculation using the sampling data
in the interval equivalent to the integral multiple of the input period. Since the ASSP method
basically is able to obtain the measurement value by just performing an averaging calculation
for the interval of one period, it is effective for a short data update period or efficient
measurement of low frequency signals. If this method cannot detect the period of the set
synchronous source signal correctly, the measurement values will not be correct. Therefore, it is
necessary to check to make sure the frequency of the synchronous source signal is measured
and displayed correctly. For the notes of the settings of the synchronous source signal and
frequency filter, refer to the instruction manual.
Setting Synchronous Source
In the case of such a signal, the synchronous source is set to the current signal side with less
harmonic components. Even if harmonic components (noise) are superimposed on the current
waveforms, measurements can be stabilized by turning on the frequency filter to detect a zero
crossing reliably.
When the frequency measurement results are correct and stable, you can consider the filter
settings are right. A frequency filter also functions as a filter to detect a zero crossing of the
synchronous source. That’s why a frequency filter is also called a synchronous source filter or a
zero crossing filter.
SUPPORTS Crest Factor 6
Selecting formulas for calculating apparent power and reactive power
Calculation Method of Voltage and Current and Procedure to Set Synchronous Source
Voltage
waveform
Current
waveform
waveform
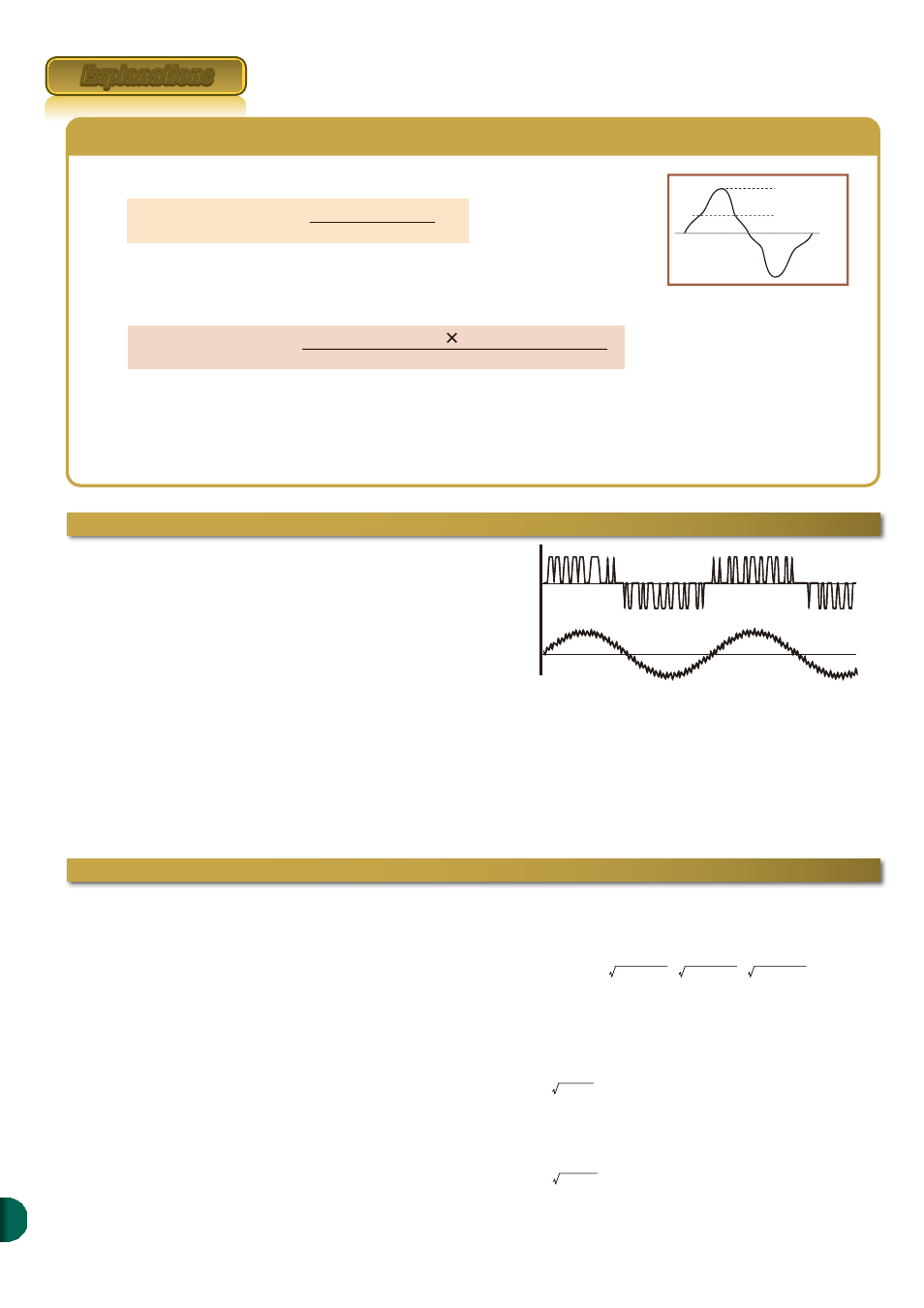
peak
RMS value
Crest factor
=
waveform peak
(CF, peak factor) RMS value
=
Crest factor (CF) =
{measuring range CF setting (3 or 6)}
measured value (RMS)
The crest factor is the ratio of the waveform peak value and the RMS value.
When checking the measurable crest factor of our power measuring instruments,
please refer to the following equation.
* However, the peak value of the measured signal must be less than or equal to the continuous maximum allowed input
* The crest factor on a power meter is specified by how many times peak input value is
allowed relative to rated input value. Even if some measured signals exist whose crest
factors are larger than the specifications of the instrument (the crest factor standard at
the rated input), you can measure signals having crest factors larger than the
specifications by setting a measurement range that is large relative to the measured
signal. For example, even if you set CF = 3, CF 5 or higher measurements are possible
as long as the measured value (RMS) is 60% or less than the measuring range. Also,
for a setting of CF = 3, measurements of CF = 300 are possible with the minimum
effective input (1% of measuring range).
There are several types of power––active power, reactive power, and apparent
power. Generally, the following equations are satisfied:
Active power P = UIcosØ
(1)
Reactive power Q = UIsinØ (2)
Apparent power S = UI (3)
In addition, these power values are related to each other as follows:
(Apparent power S)
2 = (Active power P) 2 + (Reactive power Q) 2 (4)
U : Voltage RMS
I : Current RMS
Ø : Phase between current and voltage
Three-phase power is the sum of the power values in the individual phases.
These defining equations are only valid for sinewaves. In recent years, there has
been an increase in measurements of distorted waveforms, and users are measuring
sinewave signals less frequently. Distorted waveform measurements provide
different measurement values for apparent power and reactive power depending on
which of the above defining equations is selected. In addition, because there is no
defining equation for power in a distorted wave, it is not necessarily clear which
equation is correct. Therefore, three different formulas for calculating apparent
power and reactive power for three-phase four-wire connection are provided with
the WT1800.
l TYPE1 (method used in normal mode with older WT Series models)
With this method, the apparent power for each phase is calculated from equation (3), and reactive power
for each phase is calculated from equation (4). Next, the results are added to calculate the power.
Active power:
P Σ=P1+P2+P3
Apparent power: S Σ=S1+S2+S3(=U1×I1+U2×I2+U3×I3)
Reactive power: Q Σ=Q1+Q2+Q3
*S1, S2, and S3 are calculated with a positive sign for the leading phase and a negative sign for the lagging phase.
l TYPE2
The apparent power for each phase is calculated from equation (3), and the results are added together to
calculate the three-phase apparent power (same as in TYPE1). Three-phase reactive power is calculated
from three-phase apparent power and three-phase active power using equation (4).
Active power:
P Σ=P1+P2+P3
Apparent power: S Σ=S1+S2+S3(=U1×I1+U2×I2+U3×I3)
Reactive power:
l
TYPE3 (method used in harmonic measurement mode with WT1600 and PZ4000)
This is the only method in which the reactive power for each phase is directly calculated using equation
(2). Three-phase apparent power is calculated from equation (4).
Active power:
P Σ=P1+P2+P3
Apparent power:
Reactive power: Q
Σ=Q1+Q2+Q3
(= ) (U1×I1) 2 -P1 2 + (U2×I2) 2 -P2 2 + (U3×I3) 2 -P3 2
Q Σ= SΣ 2 -P Σ 2
S Σ= PΣ 2 +Q Σ 2
14