Table 2. coefficients to calculate cf1 and cf2 – Rainbow Electronics MAX7030 User Manual
Page 14
MAX7030
Low-Cost, 315MHz, 345MHz, and 433.92MHz
ASK Transceiver with Fractional-N PLL
14
______________________________________________________________________________________
Intermediate Frequency (IF)
The IF section presents a differential 330
Ω load to pro-
vide matching for the off-chip ceramic filter. The internal
six AC-coupled limiting amplifiers produce an overall
gain of approximately 65dB, with a bandpass filter type
response centered near the 10.7MHz IF frequency with
a 3dB bandwidth of approximately 10MHz. For ASK
data, the RSSI circuit demodulates the IF to baseband
by producing a DC output proportional to the log of the
IF signal level with a slope of approximately 15mV/dB.
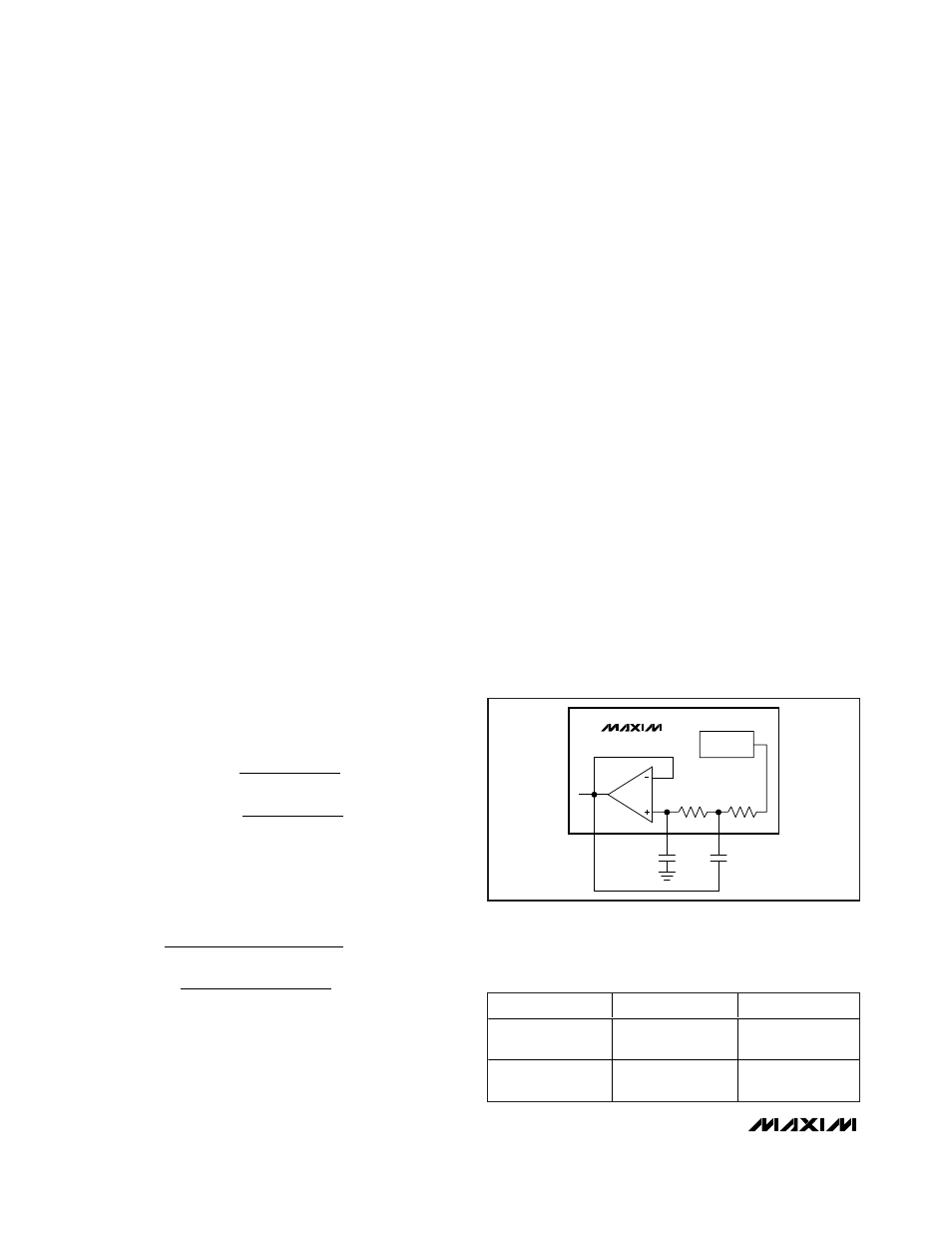
Data Filter
The data filter for the demodulated data is implemented
as a 2nd-order, lowpass, Sallen-Key filter. The pole
locations are set by the combination of two on-chip
resistors and two external capacitors. Adjusting the
value of the external capacitors changes the corner fre-
quency to optimize for different data rates. Set the cor-
ner frequency in kHz to approximately 3 times the
fastest expected Manchester data rate in kbps from the
transmitter (1.5 times the fastest expected NRZ data
rate). Keeping the corner frequency near the data rate
rejects any noise at higher frequencies, resulting in an
increase in receiver sensitivity.
The configuration shown in Figure 1 can create a
Butterworth or Bessel response. The Butterworth filter
offers a very-flat-amplitude response in the passband
and a rolloff rate of 40dB/decade for the two-pole filter.
The Bessel filter has a linear phase response, which
works well for filtering digital data. To calculate the
value of the capacitors, use the following equations,
along with the coefficients in Table 2:
where f
C
is the desired 3dB corner frequency.
For example, choose a Butterworth filter response with
a corner frequency of 5kHz:
Choosing standard capacitor values changes C
F1
to
470pF and C
F2
to 220pF. In the Typical Application Circuit,
C
F1
and C
F2
are named C16 and C17, respectively.
Data Slicer
The data slicer takes the analog output of the data filter
and converts it to a digital signal. This is achieved by
using a comparator and comparing the analog input to
a threshold voltage. The threshold voltage is set by the
voltage on the DS- pin, which is connected to the nega-
tive input of the data slicer comparator.
Numerous configurations can be used to generate the
data-slicer threshold. For example, the circuit in
Figure
2 shows a simple method using only one resistor and
one capacitor. This configuration averages the analog
output of the filter and sets the threshold to approxi-
mately 50% of that amplitude. With this configuration,
the threshold automatically adjusts as the analog signal
varies, minimizing the possibility for errors in the digital
data. The values of R and C affect how fast the thresh-
old tracks the analog amplitude. Be sure to keep the
corner frequency of the RC circuit much lower (about
10 times) than the lowest expected data rate.
With this configuration, a long string of NRZ zeros or
ones can cause the threshold to drift. This configuration
works best if a coding scheme, such as Manchester
coding, which has an equal number of zeros and ones,
is used.
Figure
3 shows a configuration that uses the positive and
negative peak detectors to generate the threshold. This
configuration sets the threshold to the midpoint between
a high output and a low output of the data filter.
C
k
kHz
pF
C
k
kHz
pF
F
F
1
2
1 000
1 414 100
3 14 5
450
1 414
4 100
3 14 5
225
=
≈
=
≈
.
( .
)(
)( .
)(
)
.
( )(
)( .
)(
)
Ω
Ω
C
b
a
k
f
C
a
k
f
F
c
F
c
1
2
100
4 100
=
Ω
=
Ω
(
)( )( )
(
)( )( )
π
π
MAX7030
RSSI
100k
Ω
C
F2
C
F1
100k
Ω
DF
OP+
DS+
Figure 1. Sallen-Key Lowpass Data Filter
FILTER TYPE
a
b
Butterworth
(Q = 0.707)
1.414
1.000
Bessel
(Q = 0.577)
1.3617
0.618
Table 2. Coefficients to Calculate CF1
and CF2
