HP 15c - Manual (Page 189)

Section 13: Finding the Roots of an Equation 189
If you have some knowledge of the behavior of the function f(x) as it varies
with different values of x, you are in a position to specify initial estimates in
the general vicinity of a zero of the function. You can also avoid the more
troublesome ranges of x such as those producing a relatively constant
function value or a minimum of the function's magnitude.
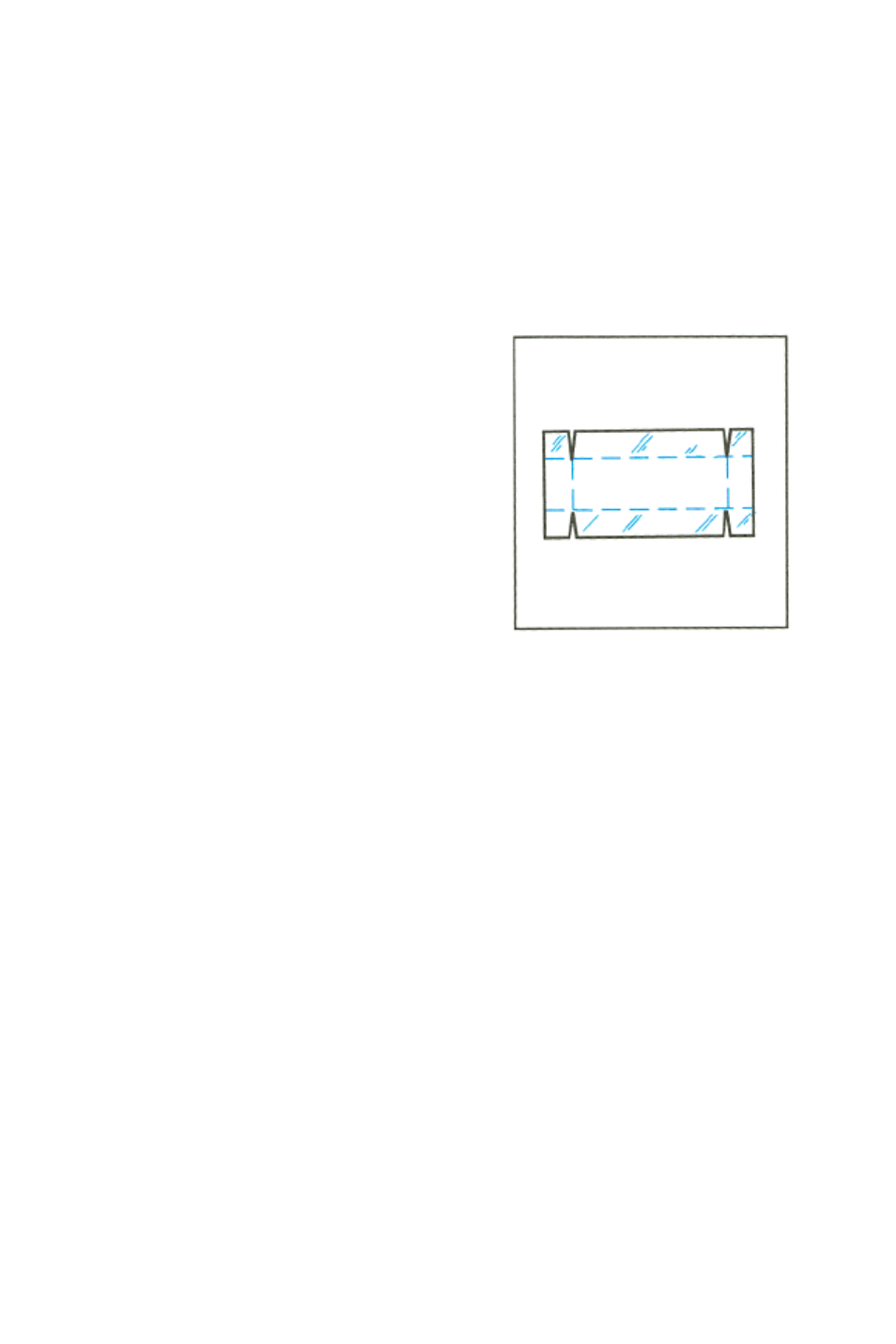
Example: Using a rectangular piece
of sheet metal 4 decimeters by 8
decimeters, an open-top box having a
volume of 7.5 cubic decimeters is to
be formed. How should the metal be
folded? (A taller box is preferred to a
shorter one.)
Solution: You need to find the height
of the box (that is, the amount to be
folded up along each of the four sides)
that gives the specified volume. If x is
the height (or amount folded up), the
length of the box is (8 – 2x) and the width is (4 – 2x). The volume V is
given by
V = (8 – 2x)(4 – 2x) x.
By expanding the expression and then using Horner's method (page 79), this
equation can be rewritten as
V = 4 ((x – 6) x + 8) x.
To get V= 7.5, find the values of x for which
f(x) = 4 ((x – 6) x + 8) x – 7.5 = 0.
The following subroutine calculates f(x):
Keystrokes Display
| ¥ 000–
Program mode.
´b 3 001–42,21, 3 Label.
6
002– 6 Assumes stack loaded with x.