HP 15c User Manual
Page 150
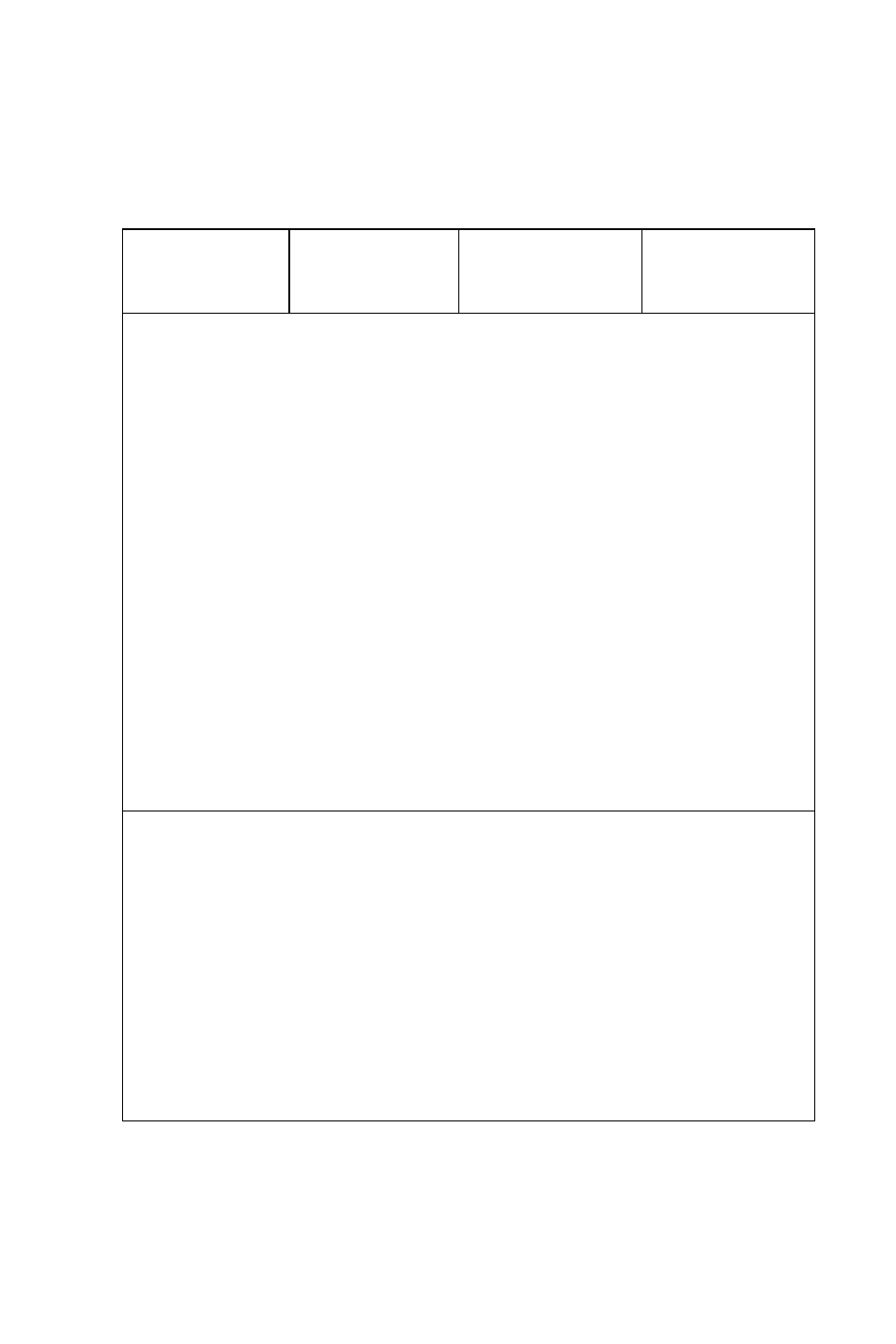
150 Section 12: Calculating with Matrices
One-Matrix Operations:
Sign Change, Inverse, Transpose, Norms, Determinant
Keystroke(s)
Result in
X-register
Effect on Matrix
Specified in
X-register
Effect on Result
Matrix
“
No change.
Changes sign of
all elements.
None. ‡
∕
(´∕ in
User Mode)
Descriptor of
result matrix.
None. ‡
Inverse of
specified matrix.
§
´>
4
Descriptor of
transpose.
Replaced by
transpose.
None. ‡
´>
7
Row norm of
specified
matrix.*
None.
None.
´>
8
Frobenius or
Euclidean norm
of specified
matrix.
†
None.
None.
´>
9
Determinant of
specified
matrix.
None.‡
LU decomposi-
tion of specified
matrix.§
*
The row norm is the largest sum of the absolute values of the elements in
each row of the specified matrix.
†
The Frobenius of Euclidean norm is the square root of the sum of the
squares of all elements in the specified matrix.
‡
Unless the result matrix is the same matrix specified in the X-register.
§
If the specified matrix is a singular matrix (that is, one that doesn’t have an
inverse), then the HP-15C modifies the LU form by an amount that is
usually small compared to round-off error. For ∕, the calculated inverse
is the inverse of a matrix close to the original, singular matrix. (Refer to the
HP-15C Advanced Functions Handbook for further information.)
