Bird Technologies VPM3 - Manual (Page 52)

44
The root sum square (RSS) uncertainty is the industry standard method for com-
bining independent uncertainties. To determine the TPS's RSS uncertainty:
1. Square each uncertainty factor.
2. Add these values together.
3. Take the square root of this sum.
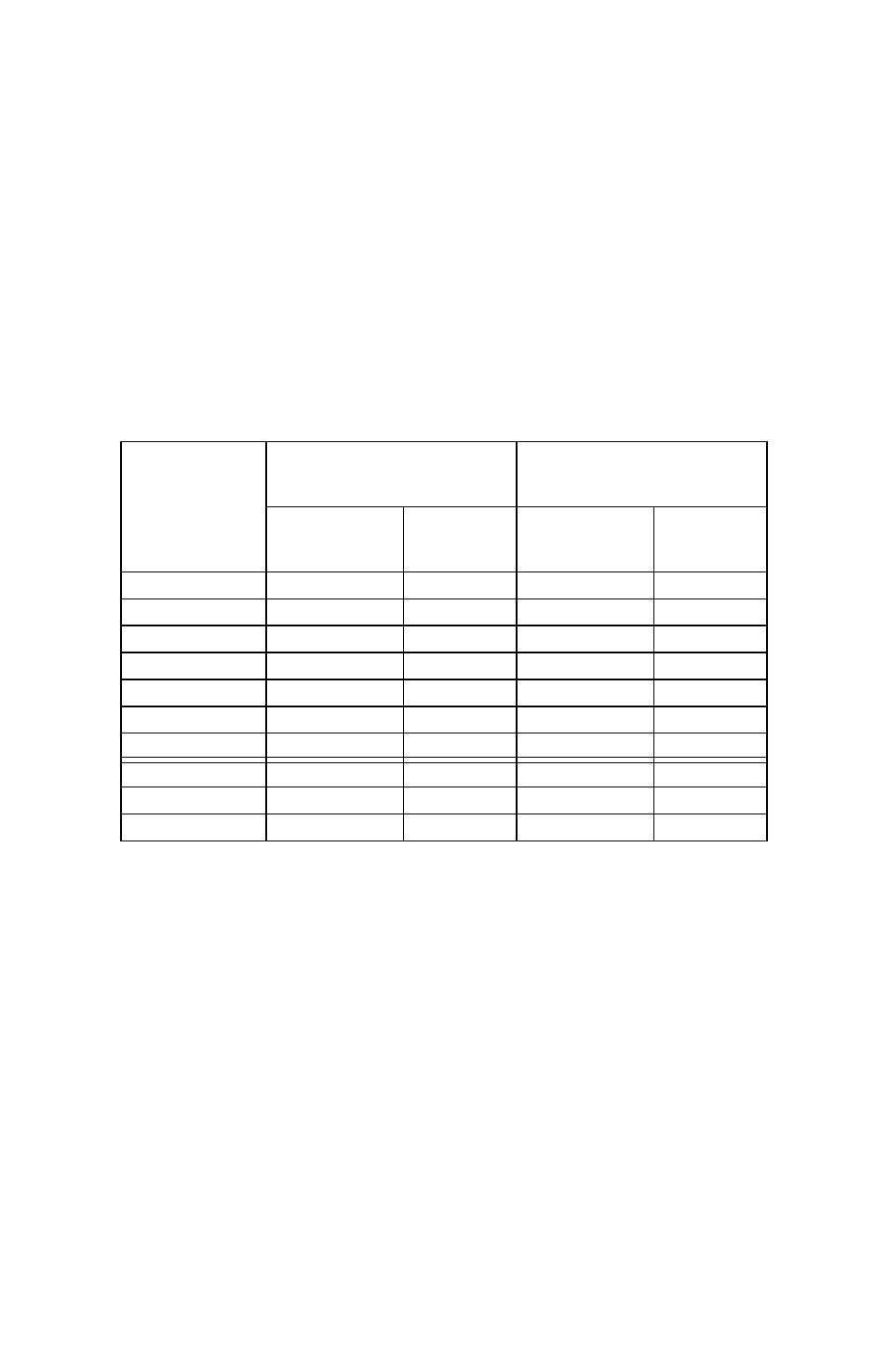
Table 3 has two examples of uncertainty calculations. The first is a 10 mW signal
at room temperature. The second is a 10 μW, 40 MHz signal at 50°C. Since this
measurement is at both low frequency and high temperature, the uncertainty
will be increased. Note that the RSS uncertainties are smaller than the values
from the rough estimate. This will always be the case.
Table 3 - Uncertainty Examples
Example 1
(10 mW, Room Temp)
Example 2
(10 μW, 40 MHz, 50°C)
Error
Source
Percent
Uncert.
RSS
Term
Percent
Uncert.
RSS
Term
Cal. Uncert. 1.13 % 1.28 1.13 % 1.28
Freq. Resp. 3.42 % 11.70 3.42 % 11.70
Temp. Lin. 3.43 % 11.76 3.43 % 11.76
Other 0.5 % 0.25 1.6 % 2.56
Res. 0.005 % 0.00 0.5 % 0.25
Zero Set 0.00125 % 0.00 1.25 % 1.56
Noise 0.007 % 0.00 2 % 4.00
Sum Uncert. 24.99 33.11
RSS Uncert. 5.00 % 5.75 %
Quick Uncert. 5.01 % 16 %
Mismatch Uncertainty
Another factor of measurement accuracy is mismatch uncertainty. When a source
and a load have different impedances, some signal will be reflected back to the
source. This uncertainty depends on both the VSWR of the TPS and the VSWR of the
rest of the system. For a system VSWR of 1.0, the mismatch uncertainty would be 0.
For a VSWR of 5.0, the mismatch uncertainty would be 12.5%. Given the VSWR of
the TPS and the source, the mismatch uncertainty can be calculated as follows.
Mismatch uncertainty (MU) is related to the reflection coefficient ( by the for-
mula:
MU percent
 
1

s

1
+
  2
1 –
  100 
=
Note:
where 
s
= reflection coefficient of the source,
and 
l
= reflection coefficient of the load (the TPS)
The reflection coefficients can be calculated from the VSWR by the formula:

VSWR 1 –
  VSWR 1
+
  
=