Casio FX-9750GII - Manual (Page 85)

2-46 46
S Formato escalonado o triangular reducido [OPTN]-[MAT]-[Rref]
Este comando utiliza el algoritmo de Gauss para triangular una matriz y darle el formato
escalonado reducido.
Ejemplo Encontrar el formato escalonado reducido de la siguiente matriz:
Matriz A =
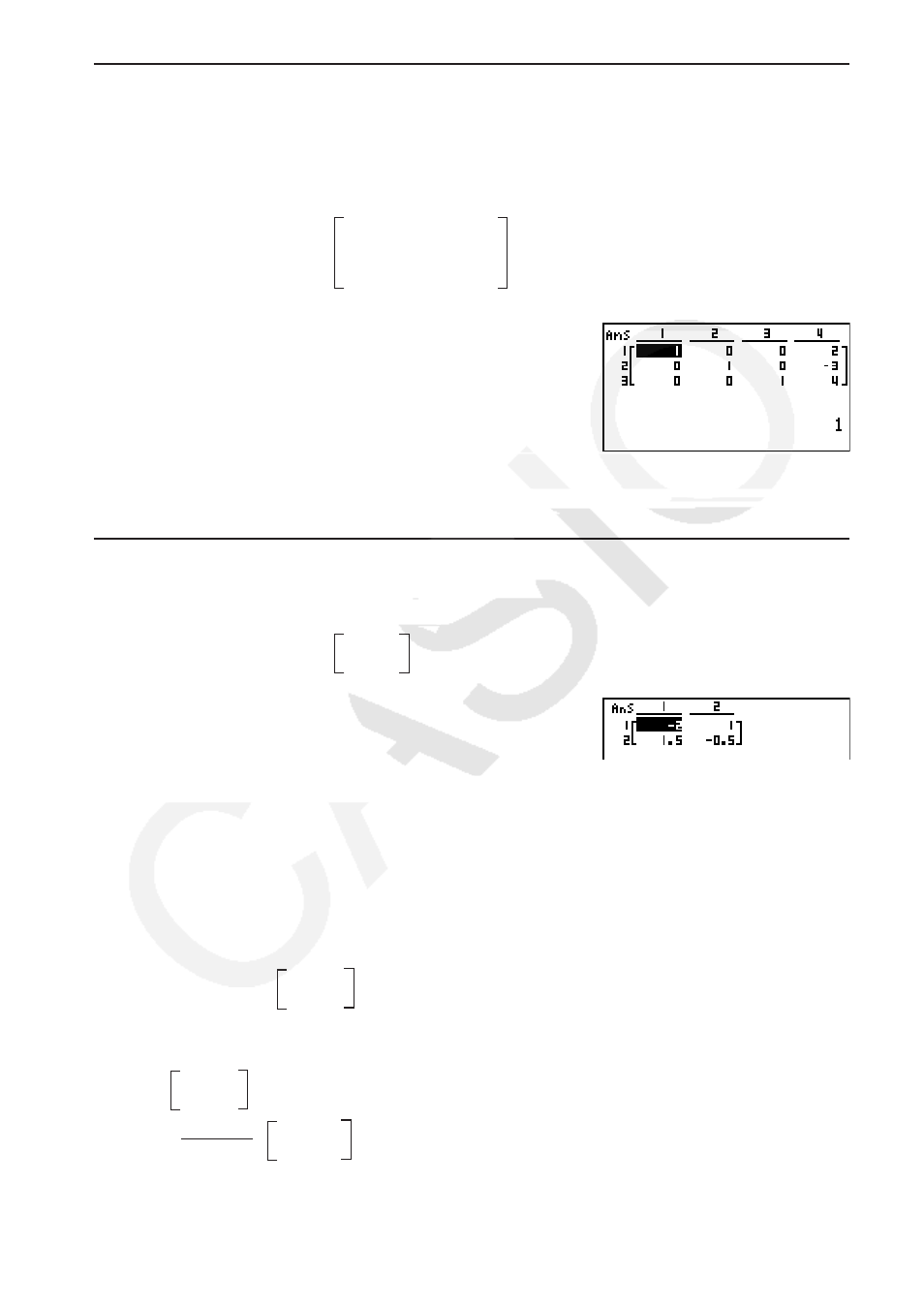
*(MAT)(E)(Rref)
(E)(Mat)?T(A)U
• Las operaciones de escalonamiento y escalonamiento reducido podrían arrojar resultados
poco precisos debido a la pérdida de dígitos.
S Inversión de matrices [ x –1 ]
Ejemplo Invertir la matriz siguiente:
Matriz A =
*(MAT)(Mat)
?T(A) x –1 ) U
• Solamente pueden invertirse matrices cuadradas (el mismo número de filas que de
columnas). Si intenta invertir una matriz que no sea cuadrada se producirá un error.
• Una matriz con determinante cero no puede ser invertida. Si intenta invertir una matriz con
determinante cero se producirá un error.
• En el caso de matrices cuyo determinante es cercano a cero la precisión del cálculo se ve
afectada.
• Para ser invertida, una matriz debe satisfacer las siguientes condiciones:
A A –1 = A –1 A = E =
1 0
0 1
A continuación se muestra la fórmula usada para invertir una matriz A y obtener su inversa
A –1 .
A =
a b
c d
A –1 =
1
ad – bc
d –b
–c a
Tenga en cuenta que ad – bc x 0.
2 −1 3 19
1 1 −5 −21
0 4 3 0
2 −1 3 19
1 1 −5 −21
0 4 3 0
1 2
3 4
1 2
3 4