Casio FX-9750GII - Manual (Page 160)

6-17 17
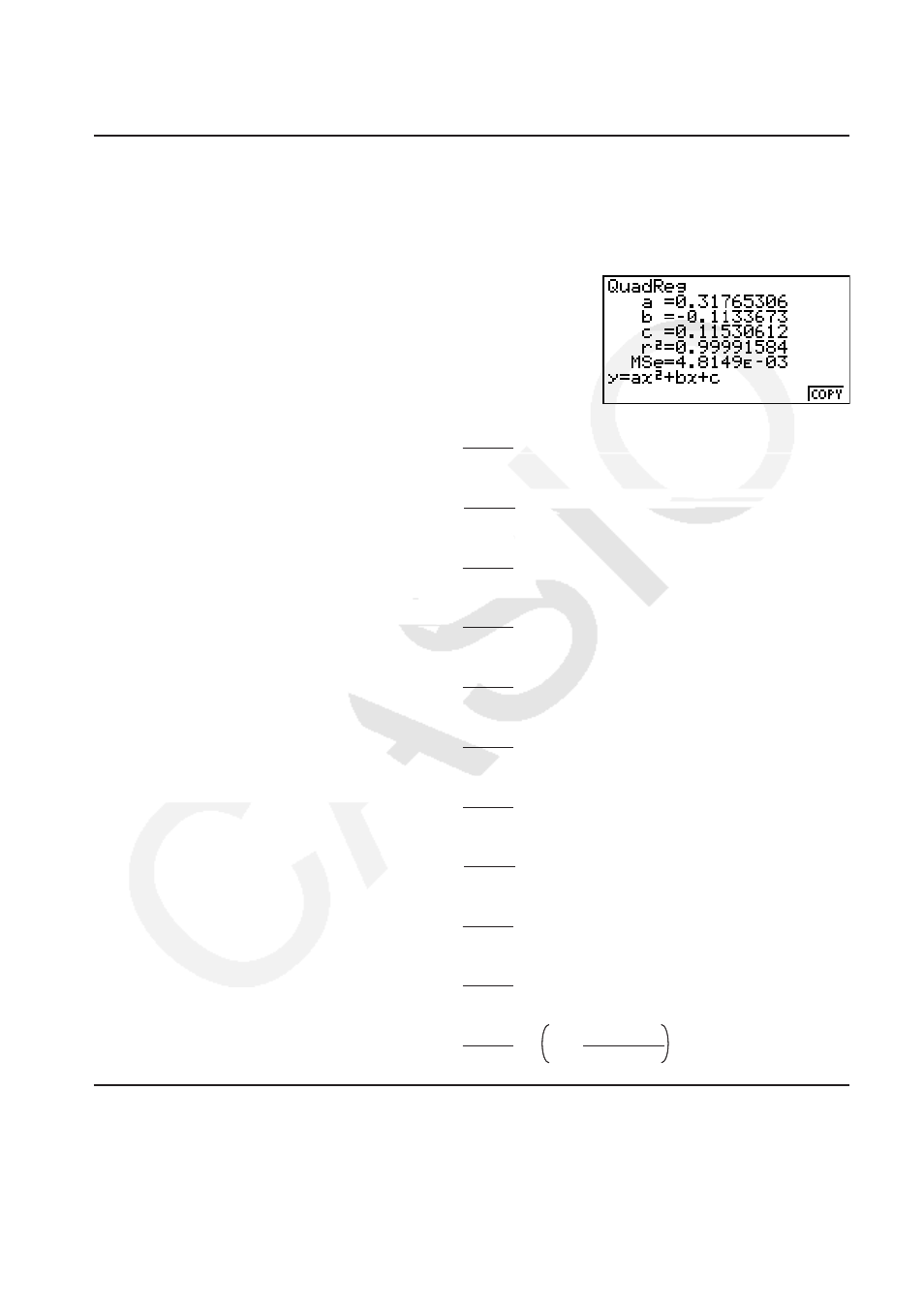
Los parámetros de esta pantalla representan lo mismo que los parámetros de los gráficos de
regresión lineal hasta regresión logística.
S Calculo del coeficiente de determinación (r 2 ) y del MSe (Error cuadrático
medio)
En modo STAT puede calcular el coeficiente de determinación(r 2 ) para las regresiones
cuadrática, cúbica y de cuarto orden. Están disponibles también, para cada tipo de regresión,
los cálculos de MSe siguientes:
• Regresión lineal ( ax + b ) ................
( a + bx ) ................
• Regresión cuadrática .....................
• Regresión cúbica ............................
• Regresión de cuarto orden .............
• Regresión logarítmica ....................
• Regresión exponencial ( a · e bx ) ........
( a · b x ) .........
• Regresión potencial ........................
• Regresión sinusoidal ......................
• Regresión logística .........................
S Cálculo del valor estimado
El modo STAT incluye la función Y-CAL que utiliza una regresión para calcular el valor
estimado de
y para un x particular luego de graficar una regresión de variables apareadas.
A continuación se muestra el procedimiento general para usar la función Y-CAL.
1. Luego de representar una gráfico de regresión, presione
ingresar al modo de selección gráfica y presione U.
MSe =
1
n – 2
i =1
n
(y
i
– (ax
i
+ b)) 2 MSe =
1
n – 2
i =1
n
(y
i
– (ax
i
+ b)) 2
MSe =
1
n – 2
i =1
n
(y
i
– (a + bx
i
)) 2 MSe =
1
n – 2
i =1
n
(y
i
– (a + bx
i
)) 2
MSe =
1
n – 3
i =1
n
(y
i
– (ax
i
+ bx
i
+ c)) 2 2 MSe =
1
n – 3
i =1
n
(y
i
– (ax
i
+ bx
i
+ c)) 2 2
MSe =
1
n – 4
i =1
n
(y
i
– (ax
i
3 + bx
i
+ cx
i
+ d )) 2 2 MSe =
1
n – 4
i =1
n
(y
i
– (ax
i
3 + bx
i
+ cx
i
+ d )) 2 2
MSe =
1
n – 5
i =1
n
(y
i
– (ax
i
4 + bx
i
3 + cx
i
+ dx
i
+ e)) 2 2 MSe =
1
n – 5
i =1
n
(y
i
– (ax
i
4 + bx
i
3 + cx
i
+ dx
i
+ e)) 2 2
MSe =
1
n – 2
i =1
n
(y
i
– (a + b ln x
i
)) 2 MSe =
1
n – 2
i =1
n
(y
i
– (a + b ln x
i
)) 2
MSe =
1
n – 2
i =1
n
(ln y
i
– (ln a + bx
i
)) 2 MSe =
1
n – 2
i =1
n
(ln y
i
– (ln a + bx
i
)) 2
MSe =
1
n – 2
i =1
n
(ln y
i
– (ln a + (ln b) · x
i
)) 2 MSe =
1
n – 2
i =1
n
(ln y
i
– (ln a + (ln b) · x
i
)) 2
MSe =
1
n – 2
i =1
n
(ln y
i
– (ln a + b ln x
i
)) 2 MSe =
1
n – 2
i =1
n
(ln y
i
– (ln a + b ln x
i
)) 2
MSe =
1
n – 2
i =1
n
(y
i
– (a sen (bx
i
+ c) + d )) 2 MSe =
1
n – 2
i =1
n
(y
i
– (a sen (bx
i
+ c) + d )) 2
MSe =
1
n – 2 1 + ae –bx
i
C
i =1
n
y
i
–
2
MSe =
1
n – 2 1 + ae –bx
i
C
i =1
n
y
i
–
2