Rice Lake Z6 Single-Ended Beam, SS Welded-seal, IP67, OIML C3 - Manual (Page 49)

Calculating Thermal Expansion of Vessels and Stay Rods 45
21.0 Calculating Thermal Expansion of Vessels and Stay Rods
21.1 Stay Rod Expansion/Contraction
Stay rods attached to vessels subjected to thermal changes
can introduce significant forces which affect system accuracy.
The method of attachment and the length of the stay rods
directly affect these forces.
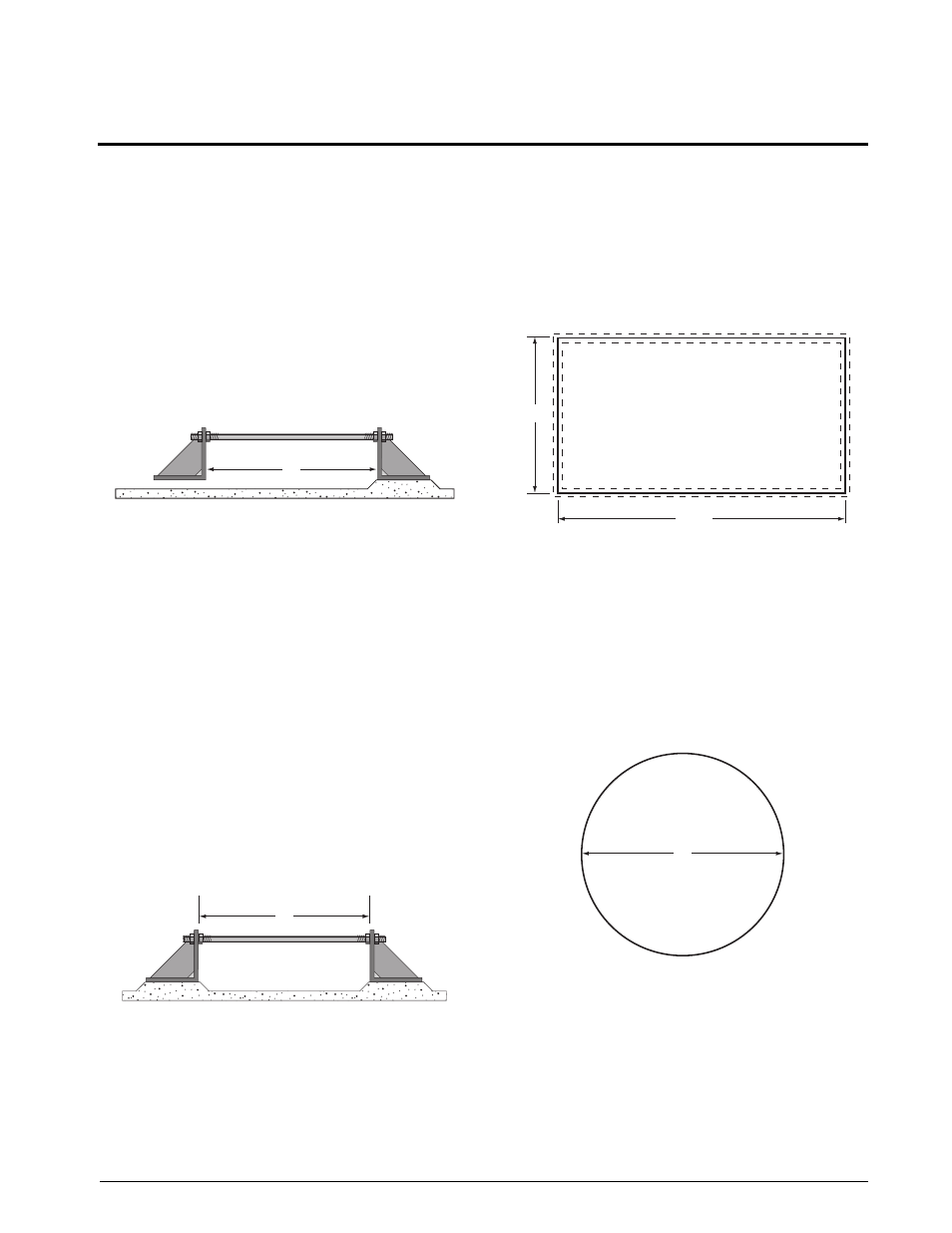
Figure 21-1 illustrates a stay rod rigidly attached to a bracket
on each end—one bracket is rigidly mounted, the other is
unattached, thus allowing the rod to expand and contract
freely. As the temperature rises or drops, the length of the rod
will increase or decrease respectively. The change in length
(ΔL) is proportional to the original length (L), the change in
temperature (ΔT), and the coefficient of linear expansion (a)
which is a characteristic of the rod material.
ΔL can be calculated from the following equation:
ΔL = a x L x ΔT
Figure 21-1.
The coefficient of thermal expansion (a) for various materials is
used to construct vessels and stay rods.
Example:
If the rod in Figure 21-2 is made from 1018 steel, then a = 6.5
x 10-6. If the rod is 48" long and the temperature increases by
60°F, the length of the rod will increase by:
ΔL = a x L x ΔT
ΔL = 6.5 x 10-6 x 48" x 60
ΔL = .019
This shows that a 48" steel rod will increase by .019" as a
result of a 60°F temperature rise. This may seem insignificant,
until you consider the forces which can result if the stay rod is
confined rigidly at each end, as in Figure 21-3
In Figure 21-2, a 1" steel rod 48" long is attached to a bracket
on each end, and both brackets are rigidly attached. If the rod
is initially adjusted so that there is no strain, a subsequent
60°F rise in temperature will cause the rod to exert a force of
9,000lb on each bracket. Hence, vessel restraint systems
must be designed and installed properly so that they don’t
move and/or apply large lateral forces to the weigh vessel.
Figure 21-2.
21.2 Vessel Expansion/Contraction
Temperature fluctuations will cause weigh vessels to grow and
contract. Figure 21-3 best illustrates this.
Shown is a top view of a rectangular vessel. The solid line
represents its size at 70°F and the inner and outer broken
lines represent its size at 40°F and 100°F respectively. The
amount that the sides will increase/decrease in length can be
found using the expansion formula discussed previously.
Therefore: ΔL = X x L x ΔT
Figure 21-3.
If the vessel is made from mild steel, the length will vary by ±
.028" (6.5 x 10-6 x 144 x 30), and the width will vary by ± .016"
(6.5 x 10-6 x 84 x 30) as the temperature fluctuates by ± 30°F.
It will be apparent that if the load cell is held rigidly by the
mount, enormous side forces will be applied to the cell, hence
the need to use a mount which can accommodate vessel
expansion/contraction due to changes in temperature.
In the case of a cylindrical vessel Figure 21-4, the change in
diameter (ΔD) resulting from a change in temperature (ΔT)
is given by:
ΔD = a x D x ΔT
Figure 21-4.
Example:
If a cylindrical vessel is 96" in diameter and made from 304
stainless steel and is subjected to a temperature rise of 80°F
as the result of being filled with a hot liquid, then the diameter
will increase by:
ΔD = 9.6 x 10-6 x 96 x 80
= .074"
L
48'
1" Dia
144.0"
84.0"
D