Rice Lake Z6 Single-Ended Beam, SS Welded-seal, IP67, OIML C3 - Manual (Page 13)

Load Cell Electrical Theory 9
6.0 Load Cell Electrical Theory
6.1 Wiring
A load cell may have a cable with four or six wires. A six-wire
load cell, besides having + and - signal and + and - excitation
lines, also has + and - sense lines. These sense lines are
connected to the sense connections of the indicator. These
lines tell the indicator what the actual voltage is at the load
cell. Sometimes there is a voltage drop between the indicator
and load cell. The sense lines feed information back to the
indicator. The indicator either adjusts its voltage to make up
for the loss of voltage, or amplifies the return signal to
compensate for the loss of power to the cell.
Loa d c ell wires are color code d to help with proper
connections. The load cell calibration data sheet for each load
cell contains the color code information for that cell. Rice Lake
Weighing Systems also provides a load cell wiring color guide
on the back cover of our Load Cell Guide.
6.2 Calibration Data
Most load cells are furnished with a calibration data sheet or
calibration certificate. This sheet gives you pertinent data
about your load cell. The data sheet is matched to the load
cell by model number, serial number and capacity. Other
information found on a typical calibration data sheet is output
expressed in mV/V, excitation voltage, non-linearity,
hysteresis, zero balance, input resistance, output resistance,
temperature effect on both the output and zero balance,
insulation resistance and cable length. The wiring color code
is also included on the calibration data sheet.
6.3 Output
A load cell’s output is not only determined by the weight
applied, but also by the strength of the excitation voltage, and
its rated mV/V full scale output sensitivity. A typical full scale
output for a load cell is 3 millivolts/volt (mV/V). This means that
for each volt of excitation voltage applied at full scale there will
be 3 millivolts of signal output. If we have 100lbs applied to a
100lb load cell with 10 volts excitation applied the load cell
signal strength will be 30mV. That is 10V x 3 mV/V= 30 mV.
Now let’s apply only 50lbs to the cell, keeping our excitation
voltage at 10 volts. Since 50lbs is 50% or one half of full load,
the cell signal strength would be 15mV.
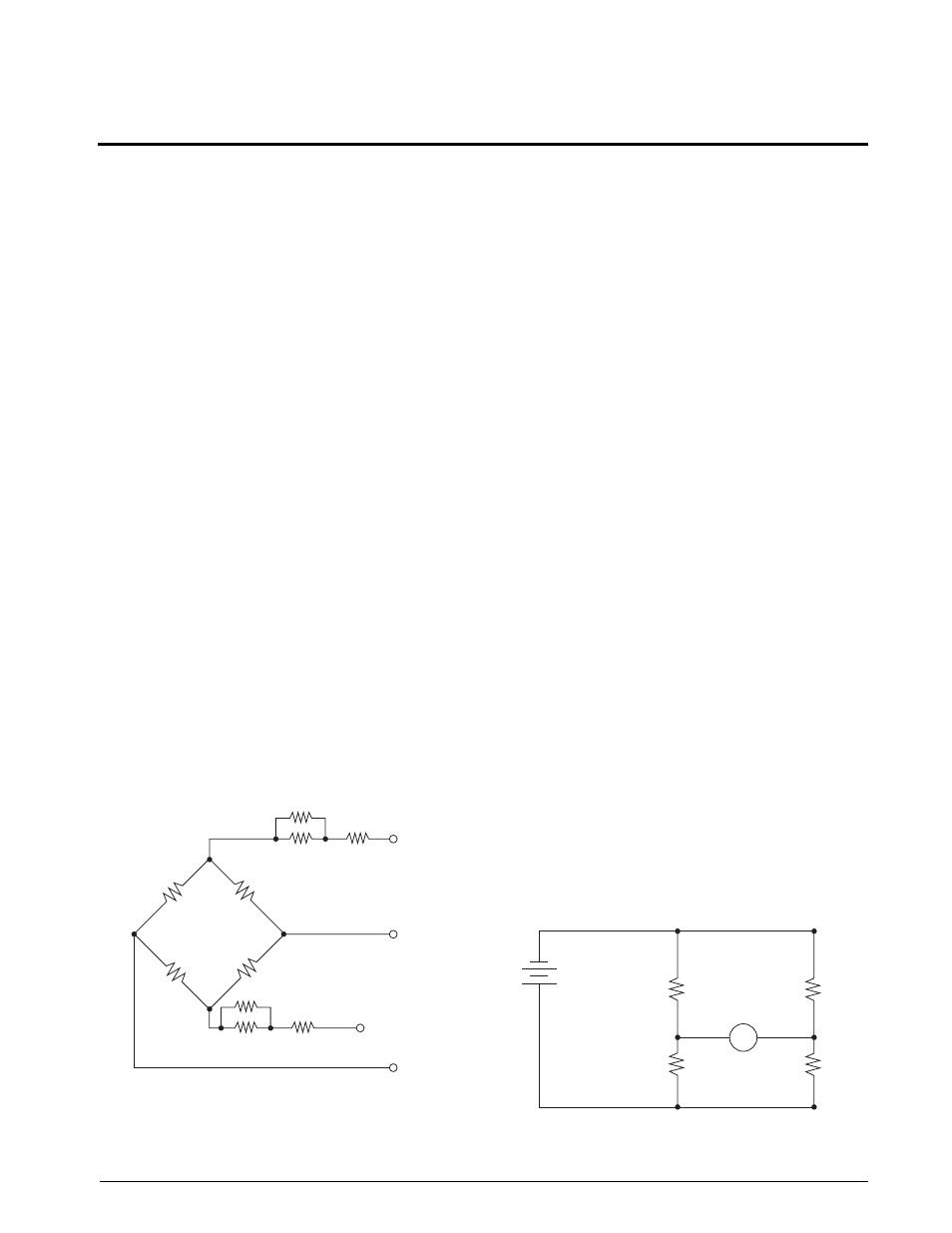
Figure 6-1. Wheatstone Bridge
The Wheatstone bridge shown in Figure 6-1 is a simple
diagram of a load cell. The resistors marked T
1
and T
2
represent strain gauges that are placed in tension when load
is applied to the cell. The resistors marked C
1
and C
2
represent strain gauges which are placed in compression
when load is applied.
The +In and -In leads are referred to as the +Excitation (+Exc)
and -Excitation (-Exc) leads. The power is applied to the load
cell from the weight indicator through these leads. The most
common excitation voltages are 10VDC, and 15VDC
depending on the indicator and load cells used. The +Out and
-Out leads are referred to as the +Signal (+Sig) and -Signal
(-Sig) leads. The signal obtained from the load cell is sent to
the signal inputs of the weight indicator to be processed and
represented as a weight value on the indicator’s digital display.
As weight is applied to the load cell, gauges C
1
and C
2
compress. The gauge wire becomes shorter and its diameter
increases. This decreases the resistances of C
1
and C
2
.
Simultaneously, gauges T
1
and T
2
are stretched. This
lengthens and decreases the diameter of T
1
and T
2
,
increasing their resistances. These changes in resistance
cause more current to flow through C
1
and C
2
and less
current to flow through T
1
and T
2
. Now a potential difference
is felt between the output or signal leads of the load cell.
Let’s trace the current flow through the load cell. Current is
supplied by the indicator through the -In lead. Current flows
from -In through C1 and through -Out to the indicator. From
the indicator current flows through the +Out lead, through C2
and back to the indicator at +In. In order to have a complete
circuit we needed to get current from the -In side of the power
s o u rc e ( I n d i c a t o r ) t o t h e + I n s i d e . Yo u c a n s e e w e
accomplished that. We also needed to pass current through
the indicator’s signal reading circuitry. We accomplished that
as the current passed from the -Out lead through the indicator
and back to the load cell through the +Out lead. Because of
the high internal impedance (resistance) of the indicator, very
little current flows between -Out and +Out.
Since there is a potential difference between the -In and +In
leads, there is still current flow from -In through T
2
and C
2
back to +In, and from -In through C
1
and T
1
back to +In. The
majority of current flow in the circuit is through these parallel
paths. Resistors are added in series with the input lines. These
resistors compensate the load cell for temperature, correct
zero and linearity.
Let’s look at a load cell bridge circuit in mathematical terms to
help you understand the bridge circuit in both a balanced and
unbalanced condition. Our Wheatstone bridge can either be
drawn in a conventional diamond shape or as shown in
Figure 6-2. Either way, it is the same circuit.
Figure 6-2. Wheatstone Bridge
58Ω
30Ω 10Ω
58Ω
30Ω 10Ω
-In (-Exc)
+Out (+Sig)
+In (+Exc)
-Out (-Sig)
T
2
350.5Ω C
1
349.5Ω
T
1
350.5Ω
C
2
349.5Ω
V
-Exc
10V
+Exc
1 2
+Sig -Sig
R
1
350Ω R
3
350Ω
R
4
350Ω R
2
350Ω