HP 15c - Manual (Page 87)

Section 4: Using Matrix Operations 87
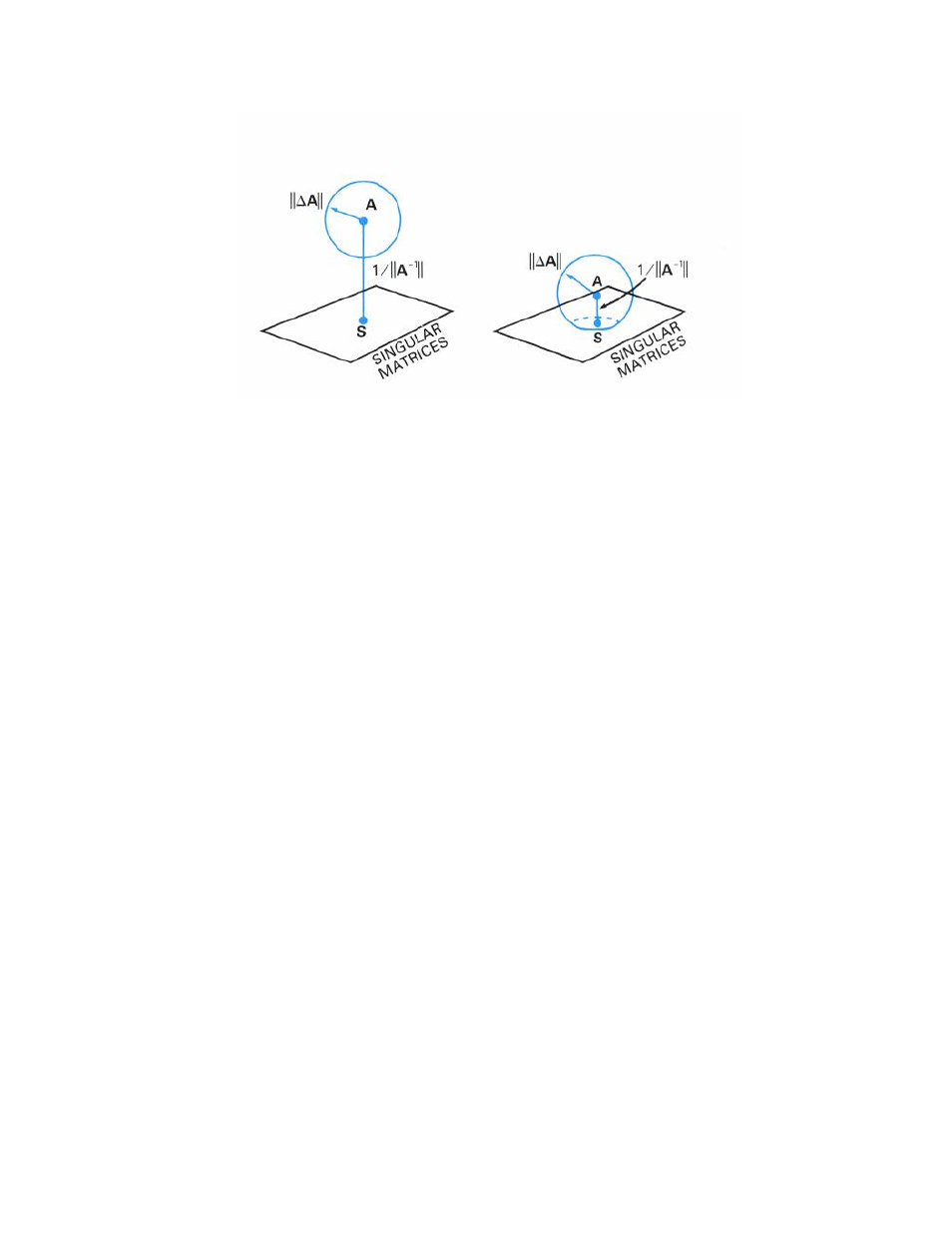
In the left diagram, ||ΔA|| < 1/||A
−1
||. If ||ΔA|| << 1 / ||ΔA
−1
|| (or K(A) ||ΔA||/||A|| << 1), then
relative variation in A
−1
= ||change in A
−1
||/||A
−1
||
≈ (||ΔA||/||A||) K(A)
= ||ΔA||/(1/||A
−1
||)
= (radius of sphere)/(distance to surface)
In the right diagram, ||ΔA||>1/||A
−1
||. In this case, there exists a singular matrix that is
indistinguishable from A, and it may not even be reasonable to try to compute the inverse of
A.
The Accuracy of Numerical Solutions to Linear Systems
The preceding discussion dealt with how uncertainties in the data are reflected in the
solutions of systems of linear equations and in matrix inverses. But even when data is exact,
uncertainties are introduced in numerically calculated solutions and inverses.
Consider solving the linear system AX = B for the theoretical solution X. Because of
rounding errors during the calculations, the calculated solution Z is in general not the
solution to the original system AX = B, but rather the solution to the perturbed system
(A + ΔA)Z = B. The perturbation ΔA satisfies ||ΔA|| < ε||A||, where ε is usually a very small
number. In many cases, ΔA will amount to less than one in the 10th digit of each element of
A.
For a calculated solution Z, the residual is R =

− AZ. Then ||R||≤ ε||A||||Z||. So the expected
residual for a calculated solution is small. But although the residual R is usually small, the
error Z − X may not be small if A is ill-conditioned:
||Z − X|| ≤ ε||A|| ||A
−1
|| ||Z|| = ε K(A) ||Z||.
A useful rule-of-thumb for the accuracy of the computed solution is