Using _ and f in complex mode, Accuracy in complex mode – HP 15c User Manual
Page 63
Section 3: Calculating in Complex Mode
63
Using
_ and f in Complex Mode
The _
and f functions use algorithms that sample your function at values along the
real axis. In Complex mode, the _
and f functions operate with only the real stack,
even though your function subroutine may have complex computations in it.
For example, _
will not search for the roots of a complex function, but rather will
sample the function on the real axis and search for a zero of the function's real part.
Similarly, f computes the integral of the function's real part along an interval on the real
axis. These operations are useful in various applications, such as calculating contour integrals
and complex potentials. (Refer to Applications at the end of this section.)
Accuracy in Complex Mode
Because complex numbers have both real components and imaginary components, the
accuracy of complex calculations takes on another dimension compared to real-valued
calculations.
When dealing with real numbers, an approximation X is close to x if the relative difference
E(X,x) = |(X − x)/x| is small. This relates directly to the number of correct significant digits of
the approximation X. That is, if E(X,x) < 5×10
−n
, then there are at least n significant digits.
For complex numbers, define E(Z,z) = |(Z - z)/z|. This does not relate directly to the number
of correct digits in each component of Z, however.
For example, if E(X,x) and E(Y,y) are both small, then for z = x + iy, E(Z,z) must also be
small. That is, if E(X,x) < s and E(Y,y) < s, then E(Z,z) < s. But consider z = 10
10
+ i and Z =
10
10
. The imaginary component of Z is far from accurate, and yet E(Z,z) < 10
−10
. Even though
the imaginary components of z and Z are completely different, in a relative sense z and Z are
extremely close.
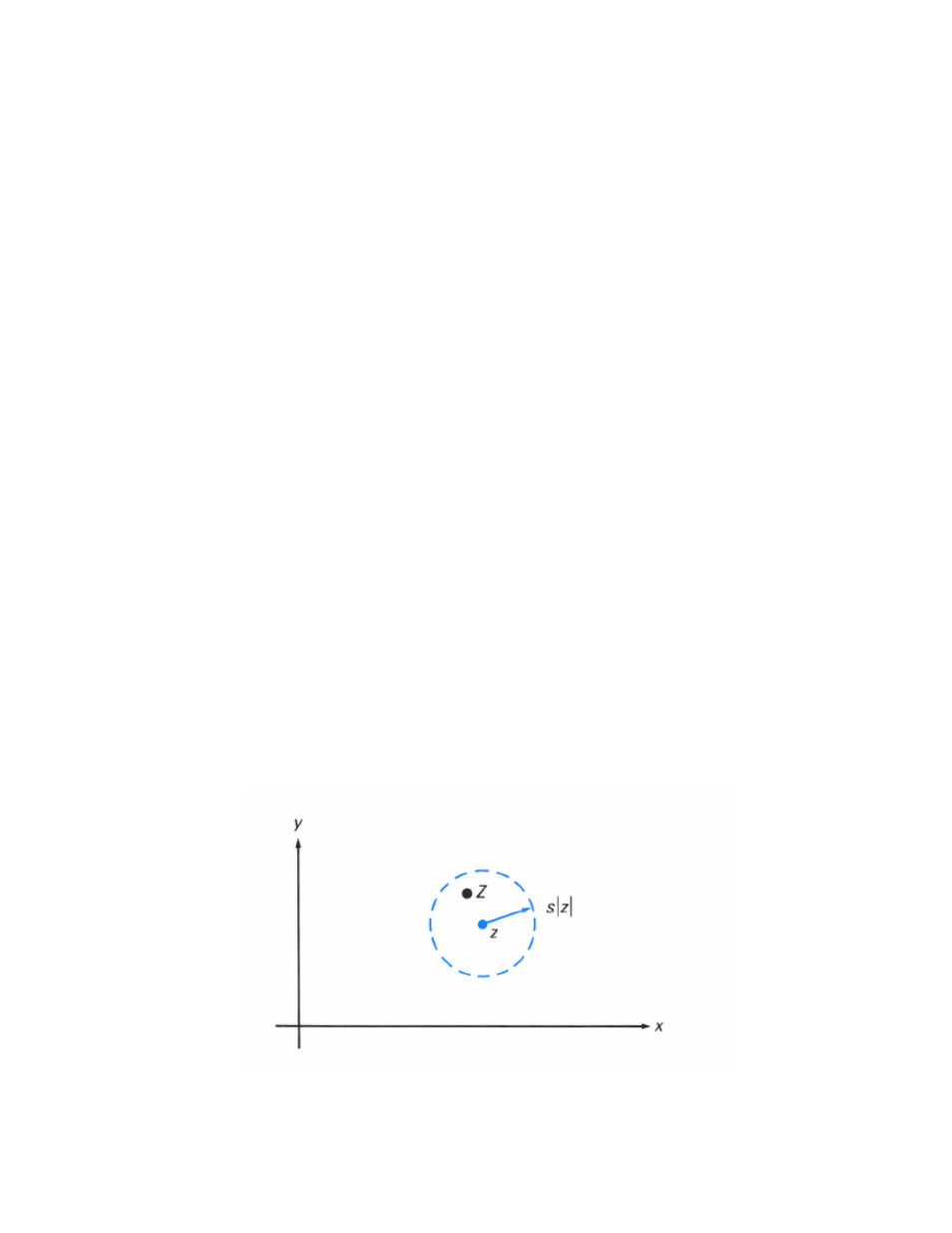
There is a simple, geometric interpretation of the complex relative error. Any approximation
Z of z satisfies E(Z,z) < s (where s is a positive real number) if and only if Z lies inside the
circle of radius s|z| centered at z in the complex plane.
